
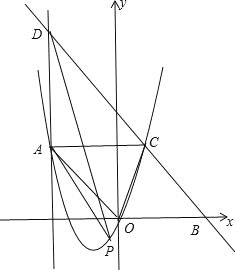
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx经过点A(﹣3,4),直线l与x轴相交于点B,与∠AOB的平分线相交于点C,直线l的解析式为y=kx﹣5k(k≠0),BC=OB.
(1)若点C在此抛物线上,求抛物线的解析式;
(2)在(1)的条件下,过点A作y轴的平行线,与直线l相交于点D,设P为抛物线上的一个动点,连接PA、PD,当![]() 时,求点P的坐标.
时,求点P的坐标.

【答案】(1)y=![]() x2+
x2+![]() x;(2)(﹣1,0)或(﹣5,
x;(2)(﹣1,0)或(﹣5,![]() )
)
【解析】
试题分析:(1)如图,先求出B点坐标,则可得到OA=OB=5,再证明AO∥CB,加上OB=BC=5,则可判断四边形AOBC为平行四边形,所以AC∥OB,AC=OB=5,于是得到C(2,4),然后利用待定系数法求抛物线解析式;
(2)如图,先确定直线l的解析式为y=﹣![]() x+
x+![]() ,再确定D点坐标,则可求出AD的长,设P(t,
,再确定D点坐标,则可求出AD的长,设P(t,![]() t2+
t2+![]() t),利用三角形面积公式和
t),利用三角形面积公式和![]() 得到
得到![]()
![]() |t+3|=
|t+3|=![]()
![]() 54,然后解绝对值方程求出t的值,从而可确定点P的坐标.
54,然后解绝对值方程求出t的值,从而可确定点P的坐标.
试题解析:(1)如图,A(﹣3,4),
∴OA=![]() =5,
=5,
当y=0时,kx﹣5k=0,解得x=5,则B(5,0),
∵BC=BO=5,
∴∠BOC=∠BCO,
∵OC平分∠AOB,
∴∠AOC=∠BOC,
∴∠AOC=∠BCO,
∴AO∥CB,
而OA=BC=5,
∴四边形AOBC为平行四边形,
∴AC∥OB,AC=OB=5,
∴C(2,4),
把A(﹣3,4),C(2,4)代入y=ax2+bx得![]() ,
,
解得a=![]() ,b=
,b=![]() ,
,
∴抛物线的解析式为y=![]() x2+
x2+![]() x;
x;
(2)如图,把C(2,4)代入y=kx﹣5k得2k﹣5k=4,解得k=﹣![]() ,
,
∴直线l的解析式为y=﹣![]() x+
x+![]() ,
,
当x=﹣2时,y=﹣![]() x+
x+![]() =
=![]() ,则D(﹣3,
,则D(﹣3,![]() ),
),
∴AD=![]() ﹣4=
﹣4=![]() ,
,
设P(t,![]() t2+
t2+![]() t),
t),
∵![]() ,
,
∴![]()
![]() |t+3|=
|t+3|=![]()
![]() 54,解得t=﹣1或t=﹣5,
54,解得t=﹣1或t=﹣5,
∴点P的坐标为(﹣1,0)或(﹣5,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2020年是具有里程碑意义的一年,我们将全面建成小康社会,全面建设小康社会的基本标准包括:人均国内生产总值超过3000美元、城镇居民人均可支配收入1.8万元等十个方面.数据“1.8万元”用科学技术法表示为( ).
A.1.8×103元B.1.8×104元C.0.18×105元D.18000元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 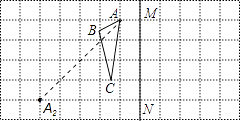
(1)请画出△ABC关于直线MN的对称图形△A1B1C1 .
(2)如果点A2是点A关于某点成中心对称,请标出这个对称中心O,并画出△ABC关于点O成中心对称的图形△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列去括号中,正确的是( )
A.a﹣(b﹣c)=a﹣b﹣c
B.c+2(a﹣b)=c+2a﹣b
C.a﹣(b﹣c)=a+b﹣c
D.a﹣(b﹣c)=a﹣b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌椅,准备修理.现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修理桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元的修理费.
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a,由甲单独修理;b,由乙单独修理;c,甲、乙合作同时修理.你认为哪种方案省时又省钱?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】洋洋有4张卡片写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题: ![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,如何抽取?最大值是多少?
(2)从中取出2张卡片,使这2张卡片上数字组成一个最大的数,如何抽取?最大的数是多少?
(3)将这4张卡片上的数字用学过的运算方法,使结果为24.写出运算式子(一种即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为﹣10,B点对应的数为70 ![]()
(1)请写出AB的中点M对应的数
(2)现在有一只电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2个单位/秒的速度向左运动,设两只电子蚂蚁在数轴上的C点相遇,请你求出C点对应的数
(3)若当电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2单位/秒的速度向左运动,经过多长时间两只电子蚂蚁在数轴上相距35个单位长度,并写出此时P点对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为体现社会对老师的尊重,教师节这一天上午,出租车司机小王在东西向的公路上免费接送老师,如果规定向东为正,向西为负,出租车的行程如下(单位:千米):+5,﹣4,+3,﹣10,+3,﹣9
最后一名老师送到目的地,小王距出租车出发点的距离是多少?在出发点的哪个方向?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com