
����Ŀ����ͼ��������y=��x2��2x+3��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ��㣮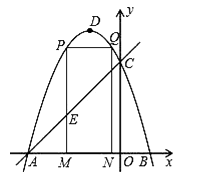
��1�����A��B��C�����ꣻ
��2����M��m��0��Ϊ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N���ɵþ���PQNM����ͼ����P�ڵ�Q��ߣ����ú�m��ʽ�ӱ�ʾ����PQNM���ܳ���
��3��������PQNM���ܳ����ʱ��m��ֵ�Ƕ��٣��������ʱ�ġ�AEM�������
��4���ڣ�3���������£�������PMNQ���ܳ����ʱ������DQ������������һ��F��y���ƽ���ߣ���ֱ��AC���ڵ�G����G�ڵ�F���Ϸ�������FG= ![]() DQ�����F�����꣮
DQ�����F�����꣮
���𰸡�
��1���⣺�������� ![]() ��֪��C��0��3����
��֪��C��0��3����
��y=0���� ![]() ��
��
���x=��3��x=1��
��A����3��0����B��1��0����
��2���⣺�������� ![]() ��֪���Գ���Ϊx=��1��
��֪���Գ���Ϊx=��1��
��M��ĺ�����Ϊm��
��PM= ![]() ��MN=����m��1����2=��2m��2��
��MN=����m��1����2=��2m��2��
�����PMNQ���ܳ�=2��PM+MN��=�� ![]() ����2=
����2= ![]() =
= ![]()
�൱m=��2ʱ���ε��ܳ����
��3���⣺�߾���PMNQ���ܳ�=2��PM+MN��=�� ![]() ����2=
����2= ![]() =
= ![]() �൱m=��2ʱ���ε��ܳ����
�൱m=��2ʱ���ε��ܳ����
��A����3��0����C��0��3������ֱ��AC����ʽΪy=kx+b�����k=1��b=3�������ʽy=x+3����x=��2ʱ����E����2��1������EM=1��AM=1����S= ![]() AMEM=
AMEM= ![]()
��4���⣺��M��ĺ�����Ϊ��2�������ߵĶԳ���Ϊx=��1����NӦ��ԭ���غϣ�Q����C���غϣ���DQ=DC����x=��1���� ![]() �����y=4����D����1��4������DQ=DC=
�����y=4����D����1��4������DQ=DC= ![]() ����FG=
����FG= ![]() DQ����FG=4����F��n��
DQ����FG=4����F��n�� ![]() ������G��n��n+3�����ߵ�G�ڵ�F���Ϸ�����
������G��n��n+3�����ߵ�G�ڵ�F���Ϸ����� ![]() =4����ã�n=��4��n=1����F����4����5����1��0����
=4����ã�n=��4��n=1����F����4����5����1��0����
����������1�����ú���ͼ����������Ľ�������������������A��B��C�����ꡣ
��2����ȷ���������߶Գ��ᣬ��M��ĺ�����Ϊm���ú�m��ʾ��PM��MN���ٸ��ݾ���PMNQ���ܳ�=2��PM+MN����������������ʽ�����ݶ��κ��������ʼ��ɵó������
��3���ɣ�2���õ��Ľ����жϳ������ܳ����ʱ��ȷ����m���������ֱ��AC����ʽ�������������ʱ�ġ�AEM�������
��4���ڣ�3���Ļ����ϣ��жϳ�NӦ��ԭ���غϣ�Q����C���غϣ����DQ=DC=![]() �����FG�ij������F�����꼰��G�����꣬����FG�ij�=4���������̣��ⷽ�����n��ֵ���Ϳ������F�����ꡣ
�����FG�ij������F�����꼰��G�����꣬����FG�ij�=4���������̣��ⷽ�����n��ֵ���Ϳ������F�����ꡣ


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�IJ���ʽx�� ![]() ��1�Ľ⼯Ϊx��1�������x��һԪ���η���x2+ax+1=0��������ǣ� ��
��1�Ľ⼯Ϊx��1�������x��һԪ���η���x2+ax+1=0��������ǣ� ��
A.��������ȵ�ʵ����
B.����������ȵ�ʵ����
C.��ʵ����
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ACB�У���һ��P��AC���ƶ�����AB=AC=5��BC=6����AP+BP+CP����СֵΪ�� ��
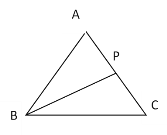
A.9.6B.9.8C.11D.10.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC����������ֱ���A(��3��2)��B(0��4)��C(0��2)��
��1������ABC�Ե�CΪ��ת������ת180�㣬������ת���Ӧ�ġ�A1B1C��ƽ�ơ�ABC������A�Ķ�Ӧ��A2������Ϊ(0����4)������ƽ�ƺ��Ӧ�ġ�A2B2C2��
��2��������A1B1C��ijһ����ת���Եõ���A2B2C2 �� ��ֱ��д����ת���ĵ����ꣻ
��3����x������һ��P��ʹ��PA��PB��ֵ��С����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�����Ϊ16��BC=8���ֽ���ABC��ֱ������ƽ��a��a��8������λ����DEF��λ�ã�

��1�����ABC��BC���ϵĸߣ�
��2������AE��AD����AB=5
�����߶�DF�ij���
�ڵ���ADE�ǵ���������ʱ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���DAB��ƽ���߽�CD��E�㣬��DE=5��EC=8��

��1������ABCD���ܳ���
��2������AC����AC=12������ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���÷�Ѵ��������Ѵָ�Ӳ�������ijˮ���ˮ�ӽ��мӸӹ̣�ר���ṩ�ķ����ǣ�ˮ�ӼӸ�2�ף���CD=2�ף�����ˮ��DE���¶�i=1��1����DB��EB=1��1������ͼ��ʾ����֪AE=4�ף���EAC=130�㣬��ˮ��ԭ���ĸ߶�BC��
���ο����ݣ�sin50���0.77��cos50���0.64��tan50���1.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B�Ƿ���������y=![]() �ڵ�һ�����ڵ�ͼ���ϵ����㣬��A��B����ĺ�����ֱ���2��4�����OAB�������_____��
�ڵ�һ�����ڵ�ͼ���ϵ����㣬��A��B����ĺ�����ֱ���2��4�����OAB�������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���AΪx�Ḻ������һ�㣬��BΪx����������һ�㣬C(0��a)��D(b��a)������a��b�����ϵʽ��|a+3|+(b-a+1)2=0.
��1��a=___��b=___����BCD�����Ϊ______��
��2����ͼ2����AC��BC����P�߶�OC��һ�㣬����BP���ӳ�BP��AC�ڵ�Q������CPQ=��CQPʱ����֤:BPƽ�֡�ABC��
��3����ͼ3����AC��BC����E�ǵ�A���B֮��һ���㣬����CE,CBʼ��ƽ�֡�ECF,����E�ڵ�A���B֮���˶�ʱ��![]() ��ֵ�Ƿ�仯�������䣬�����ֵ�����仯����˵������.
��ֵ�Ƿ�仯�������䣬�����ֵ�����仯����˵������.



�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com