
【题目】如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
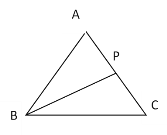
A.9.6B.9.8C.11D.10.2
【答案】B
【解析】
过点A作AD⊥BC于D,根据题意可得当BP最小时,AP+BP+CP最小,然后根据垂线段最短可得当BP⊥AC时,BP最小,然后根据三线合一和勾股定理即可求出BD和AD,然后根据S△ABC=![]() BC·AD=
BC·AD=![]() AC·BP即可求出此时的BP,从而求出结论.
AC·BP即可求出此时的BP,从而求出结论.
解:过点A作AD⊥BC于D

∵AP+CP=AC=5
∴AP+BP+CP=5+BP,即当BP最小时,AP+BP+CP最小,
根据垂线段最短,当BP⊥AC时,BP最小
∵AB=AC=5,BC=6,
∴BD=![]() BC=3
BC=3
根据勾股定理AD=![]() =4
=4
此时S△ABC=![]() BC·AD=
BC·AD=![]() AC·BP
AC·BP
∴![]() ×6×4=
×6×4=![]() ×5·BP
×5·BP
解得:BP=![]()
∴AP+BP+CP的最小值为![]() +5=
+5=![]()
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于M、N两点.
的图象交于M、N两点.
(1)利用图中条件,求反比例函数和一次函数的解析式.
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )

A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
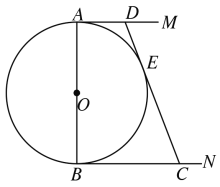
【题目】如图,![]() 的直径
的直径![]() ,
,![]() ,
,![]() 是
是![]() 的两条切线,
的两条切线,![]() 切
切![]() 于
于![]() ,交
,交![]() 于
于![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若![]() ,
,![]() 是
是![]() 的两实根,求
的两实根,求![]() ,
,![]() 的值;
的值;
(3)在(2)的前提下,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.

解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠APC与∠BAP、∠PCD之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】谁更合理?
某种牙膏上部圆的直径为2.6cm,下部底边的长为4cm,如图,现要制作长方体的牙膏盒,牙膏盒底面是正方形,在手工课上,小明、小亮、小丽、小芳制作的牙膏盒的高度都一样,且高度符合要求.不同的是底面正方形的边长,他们制作的边长如下表:
制作者 | 小明 | 小亮 | 小丽 | 小芳 |
正方形的边长 | 2cm | 2.6cm | 3cm | 3.4cm |
(1)这4位同学制作的盒子都能装下这种牙膏吗?(![]() )
)
(2)若你是牙膏厂的厂长,从节约材料又方便取放牙膏的角度来看,你认为谁的制作更合理?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.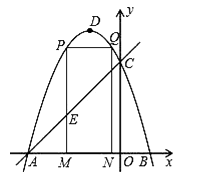
(1)求点A、B、C的坐标;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;
(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积;
(4)在(3)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG= ![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
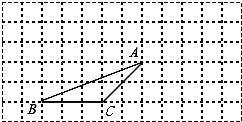
【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度。
⑴在图中画出平移后的△A′B′C′;
⑵若连接AA′、CC′,则这两条线段的关系是 ;
⑶作△ABC的高AD,并求△ABC的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com