
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于M、N两点.
的图象交于M、N两点.
(1)利用图中条件,求反比例函数和一次函数的解析式.
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.

【答案】(1)y=![]() ,y=2x-2;(2)x<-1或0<x<2.
,y=2x-2;(2)x<-1或0<x<2.
【解析】
(1)把M(2,2)代入反比例函数解析式,可求出k值,即可得反比例函数解析式;把M(2,2),N(-1,-4)代入一次函数解析式,可求出a、b的值,即可得答案;(2)观察函数图象得到当x>-1或0<x<2时,反比例函数图象都在一次函数图象上方,即反比例函数的值大于一次函数的值.
(1)∵M(2,2)在反比例函数y=![]() 的图象上,
的图象上,
∴2=![]() ,
,
解得:k=4,
∴反比例函数的解析式为:y=![]() .
.
∵M(2,2),N(-1,-4)在一次函数y=ax+b的图象上,
∴![]() ,
,
解得:![]() ,
,
∴一次函数的解析式为:y=2x-2.
(2)根据图象可知:当x>-1或0<x<2时,反比例函数图象都在一次函数图象上方,
∴反比例函数的值大于一次函数的值的x的取值范围为x<-1或0<x<2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:

∵AB∥DC( ),
∴∠1=∠CFE( ).
∵AE平分∠BAD( ),
∴∠1= ( ).
∵∠CFE=∠E( ),
∴∠2= (等量代换),
∴AD∥ ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
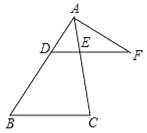
【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果![]() ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.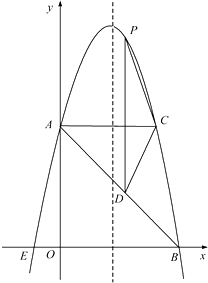
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A,E,N,M为顶点的四边形是平行四边形,且AE为其一边,求点M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大小两种货车运送360台机械设备,有三种运输方案.
方案一:设备的![]() 用大货车运送,其余用小货车运送,需要货车27辆.
用大货车运送,其余用小货车运送,需要货车27辆.
方案二:设备的![]() 用大货车运送,其余用小货车运送,需要货车28辆.
用大货车运送,其余用小货车运送,需要货车28辆.
方案三:设备的![]() 用大货车运送,其余用小货车运送,需要货车26辆.
用大货车运送,其余用小货车运送,需要货车26辆.
(1)每辆大、小货车各可运送多少台机械设备?
(2)如果大货车运费比小货车高m%(m>0),请你从中选择一种方案,使得运费最低,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的不等式x﹣ ![]() <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
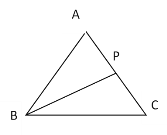
A.9.6B.9.8C.11D.10.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com