
【题目】大小两种货车运送360台机械设备,有三种运输方案.
方案一:设备的![]() 用大货车运送,其余用小货车运送,需要货车27辆.
用大货车运送,其余用小货车运送,需要货车27辆.
方案二:设备的![]() 用大货车运送,其余用小货车运送,需要货车28辆.
用大货车运送,其余用小货车运送,需要货车28辆.
方案三:设备的![]() 用大货车运送,其余用小货车运送,需要货车26辆.
用大货车运送,其余用小货车运送,需要货车26辆.
(1)每辆大、小货车各可运送多少台机械设备?
(2)如果大货车运费比小货车高m%(m>0),请你从中选择一种方案,使得运费最低,并说明理由.
【答案】(1)大货车每辆装15台,小货车每辆装12台;(2)当0<m<25,方案三运费最低;当m=25时,三种方案运费一样;当m>25时,方案二运费最低,理由见解析.
【解析】
(1)设方案一大货车有x辆,每辆装有机器 台,小货车有(27-x)辆,每辆装有机器
台,小货车有(27-x)辆,每辆装有机器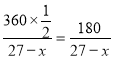 台,根据方案二列出分式方程即可求出结论;
台,根据方案二列出分式方程即可求出结论;
(2)设w1、w2、w3分别表示方案一、方案二、方案三的运费,小货车每台每次运费a(a为常数)元,分别求出w1、w2、w3与m的函数关系式,然后画出对应的图象,根据图象即可得出结论.
解:(1)设方案一大货车有x辆,每辆装有机器 台,小货车有(27-x)辆,每辆装有机器
台,小货车有(27-x)辆,每辆装有机器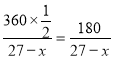 台,
台,
依题意得方程 =28,
=28,
解得x=12,
经检验:x=12是原方程的解
小货车为27-12=15(辆),
大货车每辆装180÷12=15台,
小货车每辆装180÷15=12台,
答:大货车每辆装15台,小货车每辆装12台.
(2)方案二大货车有360×![]() ÷15=8台;
÷15=8台;
方案三大货车有360×![]() ÷15=16台;
÷15=16台;
设w1、w2、w3分别表示方案一、方案二、方案三的运费,小货车每台每次运费a(a为常数)元,
方案一:w1=(27+12m%)a=12am%+27a
方案二:w2=(28+8m%)a=8am%+28a
方案三:w3=(26+16m%)a=16am%+26a
当w1= w2时,
解得:m=25;
当w1= w3时,
解得:m=25;
画出w与m的函数图象,如下所示
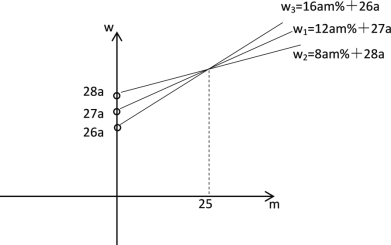
由图象可知:当0<m<25,
∴w3<w1<w2,方案三运费最低.
当m=25时,w1=w2=w3,三种方案运费一样,
当m>25时,w2<w1<w3,方案二运费最低.
答:当0<m<25,方案三运费最低;当m=25时,三种方案运费一样;当m>25时,方案二运费最低.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的四个顶点分别为
的四个顶点分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)作![]() ,使它与
,使它与![]() 关于原点
关于原点![]() 成中心对称.
成中心对称.
(2)作![]() 的两条对角线的交点
的两条对角线的交点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,点
,点![]() 的坐标为_______.
的坐标为_______.
(3)若将点![]() 向上平移
向上平移![]() 个单位,使其落在
个单位,使其落在![]() 内部(不包括边界),则
内部(不包括边界),则![]() 的取值范围是_______.
的取值范围是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于M、N两点.
的图象交于M、N两点.
(1)利用图中条件,求反比例函数和一次函数的解析式.
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用960元购进一批服装,并以每件46元的价格全部售完,由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售,卖了部分后,为了加快资金周转,服装店将剩余的20件以售价的九折全部出售.问:
(1)该服装店第一次购买了此种服装多少件?
(2)两次出售服装共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB∥OA,∠C=∠OAB=124°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF,∠OEC=∠COB,则∠OEC=______.
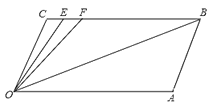
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )

A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】谁更合理?
某种牙膏上部圆的直径为2.6cm,下部底边的长为4cm,如图,现要制作长方体的牙膏盒,牙膏盒底面是正方形,在手工课上,小明、小亮、小丽、小芳制作的牙膏盒的高度都一样,且高度符合要求.不同的是底面正方形的边长,他们制作的边长如下表:
制作者 | 小明 | 小亮 | 小丽 | 小芳 |
正方形的边长 | 2cm | 2.6cm | 3cm | 3.4cm |
(1)这4位同学制作的盒子都能装下这种牙膏吗?(![]() )
)
(2)若你是牙膏厂的厂长,从节约材料又方便取放牙膏的角度来看,你认为谁的制作更合理?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com