
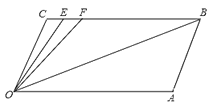
【题目】如图,CB∥OA,∠C=∠OAB=124°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF,∠OEC=∠COB,则∠OEC=______.
【答案】42°
【解析】
根据平行四边形的性质得∠OEC=∠EOB+∠AOB,∠OBA=∠BOC=∠COE+∠EOB,再根据CO∥AB,∠OEC=∠COB得∠OEC=∠COB=∠OBA,求出∠COE和∠EOB即可得出答案.
解:∵CB∥OA,∠C=∠OAB=124°,
∴∠AOC=∠ABC=56°,
则四边形AOCB为平行四边形,
则∠OEC=∠EOB+∠AOB,∠OBA=∠BOC=∠COE+∠EOB,
又∵CO∥AB,∠OEC=∠COB,
∴∠OEC=∠COB=∠OBA,
则∠AOB=∠COE,
则∠COE=∠EOF=∠FOB=∠AOB=56°÷4=14°,
则∠EOB=2×14°=28°,
此时∠OBA=∠OEC=28°+14°=42°.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0)、A(0,6)、B(4,6)、C(4,4)、D(6,4),E(6,0),若直线L经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线L的函数表达式是 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.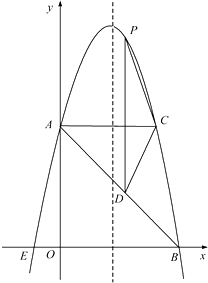
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A,E,N,M为顶点的四边形是平行四边形,且AE为其一边,求点M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大小两种货车运送360台机械设备,有三种运输方案.
方案一:设备的![]() 用大货车运送,其余用小货车运送,需要货车27辆.
用大货车运送,其余用小货车运送,需要货车27辆.
方案二:设备的![]() 用大货车运送,其余用小货车运送,需要货车28辆.
用大货车运送,其余用小货车运送,需要货车28辆.
方案三:设备的![]() 用大货车运送,其余用小货车运送,需要货车26辆.
用大货车运送,其余用小货车运送,需要货车26辆.
(1)每辆大、小货车各可运送多少台机械设备?
(2)如果大货车运费比小货车高m%(m>0),请你从中选择一种方案,使得运费最低,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给定关于 ![]() 的二次函数
的二次函数 ![]() ,
,
学生甲:当 ![]() 时,抛物线与
时,抛物线与 ![]() 轴只有一个交点,因此当抛物线与
轴只有一个交点,因此当抛物线与 ![]() 轴只有一个交点时,
轴只有一个交点时, ![]() 的值为3;
的值为3;
学生乙:如果抛物线在 ![]() 轴上方,那么该抛物线的最低点一定在第二象限;
轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的不等式x﹣ ![]() <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有形状、大小和质地都相同的四张卡片![]() ,
,![]() ,
,![]() ,
,![]() ,正面上分别写有四个实数
,正面上分别写有四个实数![]() ,
,![]() ,
,![]() ,
,![]() 将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
(1)画树形图或列表法表示抽取两张卡片可能出现的所有情况(卡片可用![]() 、
、![]() 、
、![]() 、
、![]() 表示);
表示);
(2)求取到的两个数都是无理数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2 , 请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com