
【题目】如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD= ![]() ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 . 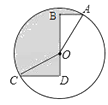
科目:初中数学 来源: 题型:
【题目】如图,将一个矩形纸片![]() ,放置在平面直角坐标系中,
,放置在平面直角坐标系中,![]() ,
,![]() 是边
是边![]() 上一点,将
上一点,将![]() 沿直线
沿直线![]() 对折,得到
对折,得到![]() .
.

(1)当![]() 平分
平分![]() 时,求
时,求![]() 的度数和点
的度数和点![]() 的坐标.
的坐标.
(2)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山脚下有一棵树AB,小强从点B沿山坡向上走50m到达点D,用高为1.5m的测角仪CD测得树顶为10°,已知山坡的坡脚为15°,则树AB的高=(精确到0.1m)(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27).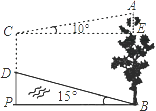
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题的提出:
如果点![]() 是锐角
是锐角![]() 内一动点,如何确定一个位置,使点
内一动点,如何确定一个位置,使点![]() 到△ABC的三顶点的距离之和
到△ABC的三顶点的距离之和![]() 的值为最小?
的值为最小?
(1)问题的转化:
把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,这样就把确定
,这样就把确定![]() 的最小值的问题转化成确定
的最小值的问题转化成确定![]() 的最小值的问题了,请你利用图1证明:
的最小值的问题了,请你利用图1证明:![]() .
.
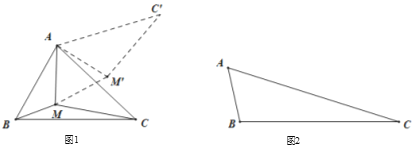
(2)问题的解决:
当点![]() 到锐角
到锐角![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小时,求
的值为最小时,求![]() 的度数.
的度数.
问题的延伸:
(3)如图2所示,在钝角![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是这个三角形内一动点,请你利用以上方法,求点
是这个三角形内一动点,请你利用以上方法,求点![]() 到这个三角形各顶点的距离之和的最小值.
到这个三角形各顶点的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于M、N两点.
的图象交于M、N两点.
(1)利用图中条件,求反比例函数和一次函数的解析式.
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB∥OA,∠C=∠OAB=124°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF,∠OEC=∠COB,则∠OEC=______.
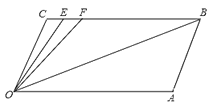
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的直径
的直径![]() ,
,![]() ,
,![]() 是
是![]() 的两条切线,
的两条切线,![]() 切
切![]() 于
于![]() ,交
,交![]() 于
于![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
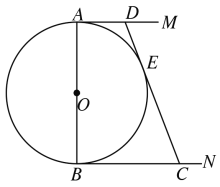
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若![]() ,
,![]() 是
是![]() 的两实根,求
的两实根,求![]() ,
,![]() 的值;
的值;
(3)在(2)的前提下,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com