
【题目】问题的提出:
如果点![]() 是锐角
是锐角![]() 内一动点,如何确定一个位置,使点
内一动点,如何确定一个位置,使点![]() 到△ABC的三顶点的距离之和
到△ABC的三顶点的距离之和![]() 的值为最小?
的值为最小?
(1)问题的转化:
把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,这样就把确定
,这样就把确定![]() 的最小值的问题转化成确定
的最小值的问题转化成确定![]() 的最小值的问题了,请你利用图1证明:
的最小值的问题了,请你利用图1证明:![]() .
.
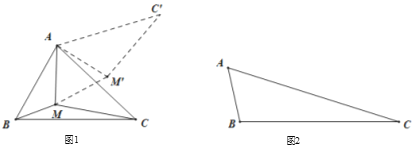
(2)问题的解决:
当点![]() 到锐角
到锐角![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小时,求
的值为最小时,求![]() 的度数.
的度数.
问题的延伸:
(3)如图2所示,在钝角![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是这个三角形内一动点,请你利用以上方法,求点
是这个三角形内一动点,请你利用以上方法,求点![]() 到这个三角形各顶点的距离之和的最小值.
到这个三角形各顶点的距离之和的最小值.
【答案】(1)证明见解析;(2)∠AMB=120°;(3)![]() .
.
【解析】
(1)证明△AMM'是等边三角形,求出MM'=MA,结合MC=M'C'可得结论;
(2)当B、M、M'、C'在同一直线上时,MA+MB+MC的值为最小,此时∠AMM'=60°,故可得∠AMB=120°;
(3)根据题意作出辅助线,利用旋转的性质求出![]() ,求得
,求得![]() 和
和![]() 的长,然后在
的长,然后在![]() 中,利用勾股定理求出
中,利用勾股定理求出![]() 的长即可.
的长即可.
(1)如图1,由旋转的性质得:∠MAM'=60°,MA=M'A,
∴△AMM'是等边三角形,
∴MM'=MA,
∵MC=M'C',
∴MA+MB+MC=BM+MM′+M′C′;
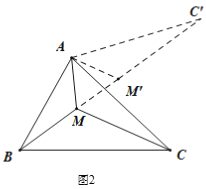
(2)如图2,把△AMC绕点A逆时针旋转60度得到△AM′C′,连接MM′,由“问题的转化”可知:当B、M、M'、C'在同一直线上时,MA+MB+MC的值为最小,
由(1)可知△AMM'是等边三角形,则∠AMM'=60°,
∴∠AMB=120°;
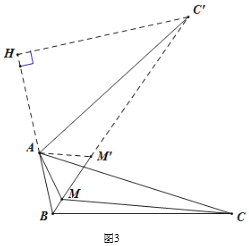
(3)如图3,把△AMC绕点A旋转60度得到△AM′C′,且B、M、M'、C'在同一直线上,过点![]() 作
作![]() 延长线的垂线
延长线的垂线![]() ,垂足为
,垂足为![]() ,
,
由旋转可得![]() ≌
≌![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,则
,则![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵点B、M、M'、C'在同一直线上,
∴在![]() 中,
中,![]() ,
,
即点![]() 到这个三角形各顶点的距离之和的最小值为
到这个三角形各顶点的距离之和的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能完全地写出来,于是小明用
的小数部分我们不可能完全地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,用这个数减去其整数部分,差就是小数部分.
的整数部分是1,用这个数减去其整数部分,差就是小数部分.
请解答下列问题:
(1)求出![]() +2的整数部分和小数部分;
+2的整数部分和小数部分;
(2)已知:10+![]() =x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数.
=x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
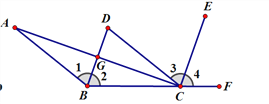
【题目】如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
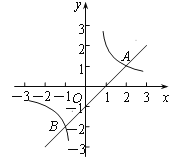
【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
(1)求m及k的值;
(2)不解关于x、y的方程组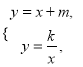 直接写出点B的坐标;
直接写出点B的坐标;
(3)直线![]() 经过点B吗?请说明理由.
经过点B吗?请说明理由.
【答案】(1)m=-1,k=2;(2)(-1,-2);(3)经过
【解析】试题分析:(1)把A(2,1)分别代入直线![]() 与双曲线
与双曲线![]() 即可求得结果;
即可求得结果;
(2)根据函数图象的特征写出两个图象的交点坐标即可;
(3)把x=-1,m=-1代入![]() 即可求得y的值,从而作出判断.
即可求得y的值,从而作出判断.
(1)把A(2,1)分别代入直线![]() 与双曲线
与双曲线![]() 的解析式得m=-1,k=2;
的解析式得m=-1,k=2;
(2)由题意得B的坐标(-1,-2);
(3)当x=-1,m=-1代入![]() 得y=-2×(-1)+4×(-1)=2-4=-2
得y=-2×(-1)+4×(-1)=2-4=-2
所以直线![]() 经过点B(-1,-2).
经过点B(-1,-2).
考点:反比例函数的性质
点评:反比例函数的性质是初中数学的重点,是中考常见题,一般难度不大,需熟练掌握.
【题型】解答题
【结束】
20
【题目】某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)
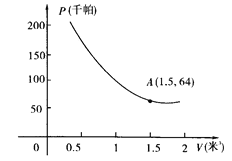
(1)写出这个函数的解析式;
(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕;
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.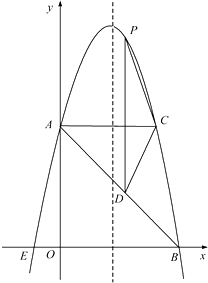
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A,E,N,M为顶点的四边形是平行四边形,且AE为其一边,求点M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给定关于 ![]() 的二次函数
的二次函数 ![]() ,
,
学生甲:当 ![]() 时,抛物线与
时,抛物线与 ![]() 轴只有一个交点,因此当抛物线与
轴只有一个交点,因此当抛物线与 ![]() 轴只有一个交点时,
轴只有一个交点时, ![]() 的值为3;
的值为3;
学生乙:如果抛物线在 ![]() 轴上方,那么该抛物线的最低点一定在第二象限;
轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)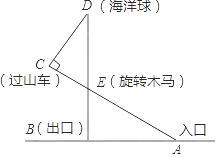
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com