
【题目】给定关于 ![]() 的二次函数
的二次函数 ![]() ,
,
学生甲:当 ![]() 时,抛物线与
时,抛物线与 ![]() 轴只有一个交点,因此当抛物线与
轴只有一个交点,因此当抛物线与 ![]() 轴只有一个交点时,
轴只有一个交点时, ![]() 的值为3;
的值为3;
学生乙:如果抛物线在 ![]() 轴上方,那么该抛物线的最低点一定在第二象限;
轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
(1)写出点A、B的坐标:A(_____,_____)、B(_____,_____);
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,写出A′、B′、C′三点坐标;
(3)求△ABC的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题的提出:
如果点![]() 是锐角
是锐角![]() 内一动点,如何确定一个位置,使点
内一动点,如何确定一个位置,使点![]() 到△ABC的三顶点的距离之和
到△ABC的三顶点的距离之和![]() 的值为最小?
的值为最小?
(1)问题的转化:
把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,这样就把确定
,这样就把确定![]() 的最小值的问题转化成确定
的最小值的问题转化成确定![]() 的最小值的问题了,请你利用图1证明:
的最小值的问题了,请你利用图1证明:![]() .
.
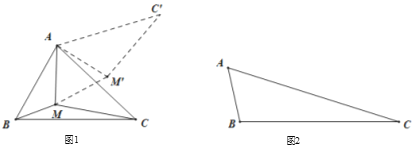
(2)问题的解决:
当点![]() 到锐角
到锐角![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小时,求
的值为最小时,求![]() 的度数.
的度数.
问题的延伸:
(3)如图2所示,在钝角![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是这个三角形内一动点,请你利用以上方法,求点
是这个三角形内一动点,请你利用以上方法,求点![]() 到这个三角形各顶点的距离之和的最小值.
到这个三角形各顶点的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.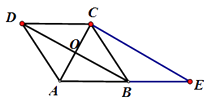
(1)求证:BD=EC;
(2)若AC=2, ![]() , 求菱形ABCD的面积.
, 求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
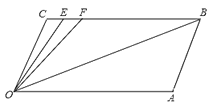
【题目】如图,CB∥OA,∠C=∠OAB=124°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF,∠OEC=∠COB,则∠OEC=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛.经过初赛、复赛,选出了两个代表队参加市内7月份的决赛.两个队各选出的![]() 名选手的复赛成绩如图所示.
名选手的复赛成绩如图所示.
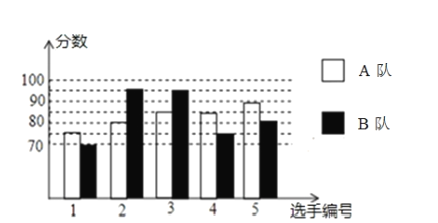
(1)根据图示补全下表;
平均数(分) | 中位数(分) | 众数(分) | |
|
|
| |
|
|
(2)结合两队成绩的平均数和中位数,分析哪个队的复赛成绩较好;
(3)计算两队成绩的方差,并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图OA平分∠BAC,∠1=∠2.
求证:AO⊥BC.
同学甲说:要作辅助线;
同学乙说:要应用角平分线性质定理来解决:
同学丙说:要应用等腰三角形“三线合一”的性质定理来解决.
请你结合同学们的讨论写出证明过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com