
【题目】已知:如图OA平分∠BAC,∠1=∠2.
求证:AO⊥BC.
同学甲说:要作辅助线;
同学乙说:要应用角平分线性质定理来解决:
同学丙说:要应用等腰三角形“三线合一”的性质定理来解决.
请你结合同学们的讨论写出证明过程.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】给定关于 ![]() 的二次函数
的二次函数 ![]() ,
,
学生甲:当 ![]() 时,抛物线与
时,抛物线与 ![]() 轴只有一个交点,因此当抛物线与
轴只有一个交点,因此当抛物线与 ![]() 轴只有一个交点时,
轴只有一个交点时, ![]() 的值为3;
的值为3;
学生乙:如果抛物线在 ![]() 轴上方,那么该抛物线的最低点一定在第二象限;
轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)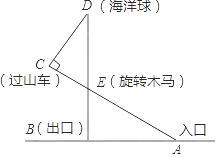
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:长方形ABCD中,点E为BC边的中点,将D折起,使点D落在点E处.

(1)请你用尺规作图画出折痕和折叠后的图形.(不要求写已知,求作和作法,保留作图痕迹)
(2)若折痕与AD、BC分别交于点M、N,与DE交于点O,求证△MDO≌△NEO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2 , 请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
请你根据上述解题思路解答下面问题:
(1)已知a﹣b=﹣3,ab=﹣2,求(a+b)(a2﹣b2)的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,∠DAB的平分线交CD于E点,且DE=5,EC=8.

(1)求□ABCD的周长;
(2)连结AC,若AC=12,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,把
,把![]() 的直角三角板
的直角三角板![]() 的直角顶点
的直角顶点![]() 放在直线
放在直线![]() 上.将直角三角板
上.将直角三角板![]() 在平面内绕点
在平面内绕点![]() 任意转动,若转动的过程中,直线
任意转动,若转动的过程中,直线![]() 与直线
与直线![]() 的夹角为60°,则
的夹角为60°,则![]() 的度数为___.
的度数为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
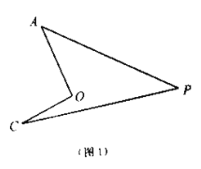
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,![]() 与
与![]() 、
、![]() 、
、![]() 的数量关系为____.
的数量关系为____.
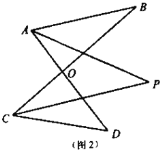
(2)如图(2),已知![]() 平分
平分![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
由(1)结论得:![]()
所以![]() 即
即![]()
因为![]()
![]()
所以![]()
所以![]() .
.
解决问题:
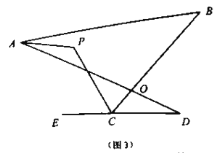
(1)如图(3),直线![]() 平分
平分![]() ,
, ![]() 平分
平分![]() 的外角
的外角![]() ,猜想
,猜想![]() 与
与![]() 、
、![]() 的数量关系是______;
的数量关系是______;
(2)如图(4),直线![]() 平分
平分![]() 的外角
的外角![]() ,
, ![]() 平分
平分![]() 的外角
的外角![]() ,猜想
,猜想![]() 与
与![]() 、
、![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com