
【题目】先化简,再求值:(x﹣1+ ![]() )÷
)÷ ![]() ,其中x的值从不等式组
,其中x的值从不等式组 ![]() 的整数解中选取.
的整数解中选取.
【答案】解:原式=( ![]() +
+ ![]() )÷
)÷ ![]()
= ![]()
![]()
= ![]()
![]()
= ![]() ,
,
解不等式组 ![]() 得:﹣1≤x<
得:﹣1≤x< ![]() ,
,
∴不等式组的整数解有﹣1、0、1、2,
∵分式有意义时x≠±1、0,
∴x=2,
则原式=0.
【解析】整式与分式相加时,整式可看作分母是1的式子,x-1=![]() ,分式的分子出现二次三项式时,可分解因式,x2-3x+2可利用十字相乘法分解为( x 1 ) ( x 2 ),也用求根公式求出可求x2-3x+2=0的根x1=1,x2=2,则x2-3x+2可分为(x-x1)(x-x2)=( x 1 ) ( x 2 ),求分式的值时,取的值一定要使原分式(最起初未化简的式子有意义,即分母不为0)有意义,因此x取2.
,分式的分子出现二次三项式时,可分解因式,x2-3x+2可利用十字相乘法分解为( x 1 ) ( x 2 ),也用求根公式求出可求x2-3x+2=0的根x1=1,x2=2,则x2-3x+2可分为(x-x1)(x-x2)=( x 1 ) ( x 2 ),求分式的值时,取的值一定要使原分式(最起初未化简的式子有意义,即分母不为0)有意义,因此x取2.
【考点精析】掌握一元一次不等式组的整数解是解答本题的根本,需要知道使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解).


科目:初中数学 来源: 题型:
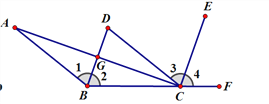
【题目】如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.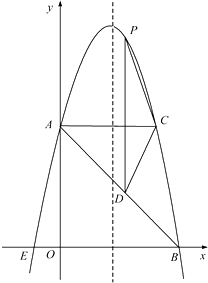
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A,E,N,M为顶点的四边形是平行四边形,且AE为其一边,求点M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给定关于 ![]() 的二次函数
的二次函数 ![]() ,
,
学生甲:当 ![]() 时,抛物线与
时,抛物线与 ![]() 轴只有一个交点,因此当抛物线与
轴只有一个交点,因此当抛物线与 ![]() 轴只有一个交点时,
轴只有一个交点时, ![]() 的值为3;
的值为3;
学生乙:如果抛物线在 ![]() 轴上方,那么该抛物线的最低点一定在第二象限;
轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的不等式x﹣ ![]() <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:解不等式 ![]() .根据两数相除,同号得正,异号得负,得不等式组
.根据两数相除,同号得正,异号得负,得不等式组 ![]() 或不等式组
或不等式组![]() 解不等式组
解不等式组 ![]() ,得
,得 ![]() ;解不等式组
;解不等式组 ![]() ,得
,得 ![]() ,所以原不等式的解集为
,所以原不等式的解集为 ![]() 或
或![]() .
.
(1)探究:解不等式 ![]() .
.
(2)应用:不等式 ![]() 的解集是 .
的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有形状、大小和质地都相同的四张卡片![]() ,
,![]() ,
,![]() ,
,![]() ,正面上分别写有四个实数
,正面上分别写有四个实数![]() ,
,![]() ,
,![]() ,
,![]() 将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
(1)画树形图或列表法表示抽取两张卡片可能出现的所有情况(卡片可用![]() 、
、![]() 、
、![]() 、
、![]() 表示);
表示);
(2)求取到的两个数都是无理数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)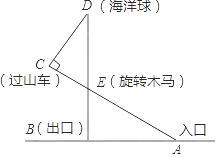
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,∠DAB的平分线交CD于E点,且DE=5,EC=8.

(1)求□ABCD的周长;
(2)连结AC,若AC=12,求□ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com