
【题目】如图,![]() 的直径
的直径![]() ,
,![]() ,
,![]() 是
是![]() 的两条切线,
的两条切线,![]() 切
切![]() 于
于![]() ,交
,交![]() 于
于![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
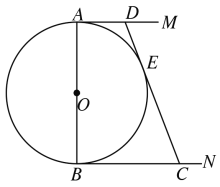
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若![]() ,
,![]() 是
是![]() 的两实根,求
的两实根,求![]() ,
,![]() 的值;
的值;
(3)在(2)的前提下,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)45
;(3)45
【解析】
(1)作DF⊥BN交BC于F;根据切线长定理得到BF=AD=x,CE=CB=y,则DC=DE+CE=x+y,在直角△DFC中根据勾股定理,就可以求出y与x的关系;
(2)由(1)求得xy=36,然后由根与系数的关系求得a的值,通过解一元二次方程即可求得x、y的值;
(3)由AM,BN是圆 O的两条切线,DC切圆 O于E,得到OE⊥CD,AD=DE,BC=CE,利用三角形面积公式即可求解.
(1)如图,作DF⊥BN交BC于F;
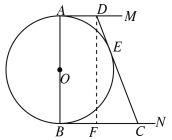
∵AM、BN与O切于点A、 B,
∴AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=12,
∵BC=y,
∴FC=BCBF=yx;
∵DE切O于E,
∴DE=DA=x,CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(yx)2+122,
整理为:![]() ,
,
∴y与x的函数关系式是![]() .
.
(2)由(1)知xy=36,
x,y是方程2t230t+a=0的两个根,
∴根据韦达定理知,xy=![]() ,即a=72;
,即a=72;
∴原方程为t215t+36=0,
解得![]() 或
或![]()
∵x<y,
∴![]() ;
;
(3)如图,连接OD,OE,OC,
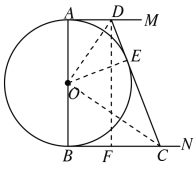
∵AD,BC,CD是圆O的切线,
∴OE⊥CD,AD=DE=3,BC=CE=12,
∴S△COD=![]()


科目:初中数学 来源: 题型:
【题目】若关于x的不等式x﹣ ![]() <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有形状、大小和质地都相同的四张卡片![]() ,
,![]() ,
,![]() ,
,![]() ,正面上分别写有四个实数
,正面上分别写有四个实数![]() ,
,![]() ,
,![]() ,
,![]() 将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
(1)画树形图或列表法表示抽取两张卡片可能出现的所有情况(卡片可用![]() 、
、![]() 、
、![]() 、
、![]() 表示);
表示);
(2)求取到的两个数都是无理数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为美化市容市貌,我市在春节前夕计划在市区几个公园建造![]() 、
、![]() 两种型号花灯供市民观赏,根据预算,共需资金
两种型号花灯供市民观赏,根据预算,共需资金![]() 万元.若建造一个
万元.若建造一个![]() 种花灯和两个
种花灯和两个![]() 类种花灯共 需资金
类种花灯共 需资金![]() 万元;建造两个
万元;建造两个![]() 种花灯和一个
种花灯和一个![]() 种花灯共需资金
种花灯共需资金![]() 万元.
万元.
(1)问建造一个![]() 种型号花灯和一个
种型号花灯和一个![]() 种型号花灯所需资金分别是多少万元?
种型号花灯所需资金分别是多少万元?
(2)若建造![]() 种型号花灯不超过
种型号花灯不超过![]() 个,则
个,则![]() 种型号花灯至少要建造多少个?
种型号花灯至少要建造多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)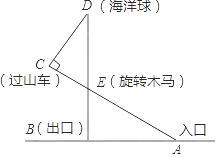
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
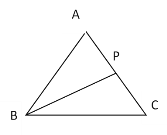
A.9.6B.9.8C.11D.10.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2 , 请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com