
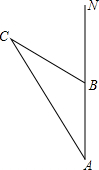
 上午6时,一条船从海岛A出发,以15海里/时的速度向正北航行,8时到达海岛B处.从A、B望灯塔C,测得∠NAC=31°,∠NBC=62°,求从海岛B到灯塔C的距离.
上午6时,一条船从海岛A出发,以15海里/时的速度向正北航行,8时到达海岛B处.从A、B望灯塔C,测得∠NAC=31°,∠NBC=62°,求从海岛B到灯塔C的距离. 科目:初中数学 来源: 题型:解答题
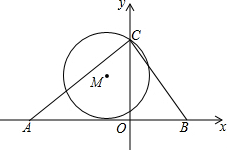 如图,在△ABC中,AB=10,AC=8,BC=6.点A、B、C都在坐标轴上.⊙M过点C且与x轴相切.设点M(x,y).
如图,在△ABC中,AB=10,AC=8,BC=6.点A、B、C都在坐标轴上.⊙M过点C且与x轴相切.设点M(x,y).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
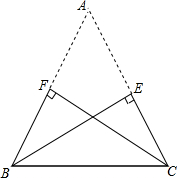 如图是缺了一个角的三角形纸片ABC,已知BE⊥AC,垂足为E,CF⊥AB,垂足为F,且BE=CF,请你根据以上条件判断△ABC的形状,并说明理由:
如图是缺了一个角的三角形纸片ABC,已知BE⊥AC,垂足为E,CF⊥AB,垂足为F,且BE=CF,请你根据以上条件判断△ABC的形状,并说明理由:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若两数相等,则它们的绝对值相等 | B. | 对顶角相等 | ||
| C. | 若a≥0,则${(\sqrt{a})}^{2}$=a | D. | 全等三角形面积相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
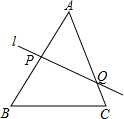 如图,直线l分别交△ABC的边AB、AC于点p、Q,若$\frac{BP}{AP}$+$\frac{CQ}{AQ}$=1.则直线1必过△ABC的( )并给予证明.(A)内心;(B)外心;(C)重心;(D)垂心.
如图,直线l分别交△ABC的边AB、AC于点p、Q,若$\frac{BP}{AP}$+$\frac{CQ}{AQ}$=1.则直线1必过△ABC的( )并给予证明.(A)内心;(B)外心;(C)重心;(D)垂心.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
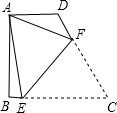 如图,在四边形ABCD中,AD∥BC,∠B=Rt∠,∠C=60°,AD=4,CD=8,点E在BC上,点F在CD上,现将四边形ABCD沿EF折叠,若点C洽与点A重合,EF为折痕,则CE=7,sin∠AFE=$\frac{5\sqrt{7}}{14}$.
如图,在四边形ABCD中,AD∥BC,∠B=Rt∠,∠C=60°,AD=4,CD=8,点E在BC上,点F在CD上,现将四边形ABCD沿EF折叠,若点C洽与点A重合,EF为折痕,则CE=7,sin∠AFE=$\frac{5\sqrt{7}}{14}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com