
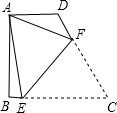
 如图,在四边形ABCD中,AD∥BC,∠B=Rt∠,∠C=60°,AD=4,CD=8,点E在BC上,点F在CD上,现将四边形ABCD沿EF折叠,若点C洽与点A重合,EF为折痕,则CE=7,sin∠AFE=$\frac{5\sqrt{7}}{14}$.
如图,在四边形ABCD中,AD∥BC,∠B=Rt∠,∠C=60°,AD=4,CD=8,点E在BC上,点F在CD上,现将四边形ABCD沿EF折叠,若点C洽与点A重合,EF为折痕,则CE=7,sin∠AFE=$\frac{5\sqrt{7}}{14}$. 分析 连接AC交EF于M,过F作FN⊥AD交AD的延长线于N,延长NF交BC于H,由折叠的性质得:EF垂直平分AC,AF=CF,根据勾股定理得到AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{48+64}$=4$\sqrt{7}$得到AM=2$\sqrt{7}$,设DF=x,根据已知条件得到DN=$\frac{1}{2}$x,NF=$\frac{\sqrt{3}}{2}$x,根据勾股定理列方程求得AF=CF=5.6,NF=$\frac{6\sqrt{3}}{5}$,于是得到sin∠AFE=$\frac{AM}{AF}$=$\frac{5\sqrt{7}}{14}$,CH=2.8,由勾股定理得到AB2+BE2=AE2,列方程求出CE=7.
解答 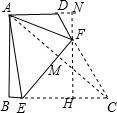 解:连接AC交EF于M,过F作FN⊥AD交AD的延长线于N,延长NF交BC于H,
解:连接AC交EF于M,过F作FN⊥AD交AD的延长线于N,延长NF交BC于H,
由折叠的性质得:EF垂直平分AC,
∴AF=CF,
∵∠B=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{48+64}$=4$\sqrt{7}$,
∴AM=2$\sqrt{7}$,
设DF=x,
∵∠BCD=60°,AD∥BC,
∴∠NDF=60°,
∴∠DFN=30°,
∴DN=$\frac{1}{2}$x,NF=$\frac{\sqrt{3}}{2}$x,
在Rt△ANF中,AN2+NF2=AF2,
即:(4+$\frac{x}{2}$)2+($\frac{\sqrt{3}x}{2}$)2=(8-x)2,
解得:x=2.4.
∴AF=CF=5.6,NF=$\frac{6\sqrt{3}}{5}$,
∴sin∠AFE=$\frac{AM}{AF}$=$\frac{5\sqrt{7}}{14}$,CH=2.8,
∴BC=8,AB=4$\sqrt{3}$,
∴AB2+BE2=AE2,
即:(4$\sqrt{3}$)2+(8-CE)2=CE2,
解得:CE=7,
故答案为:7,$\frac{{5\sqrt{7}}}{14}$,
点评 本题考查了翻折变换-折叠问题,解直角三角形,熟练掌握折叠的性质是解题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:解答题
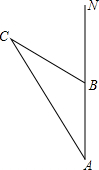 上午6时,一条船从海岛A出发,以15海里/时的速度向正北航行,8时到达海岛B处.从A、B望灯塔C,测得∠NAC=31°,∠NBC=62°,求从海岛B到灯塔C的距离.
上午6时,一条船从海岛A出发,以15海里/时的速度向正北航行,8时到达海岛B处.从A、B望灯塔C,测得∠NAC=31°,∠NBC=62°,求从海岛B到灯塔C的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
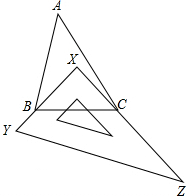 如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.
如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com