
分析 (1)前面1到9,都是一位数,故有9位,后面接下来从10到98每个数都是两位,总共有(98-9)×2=89×2=178位数,所以1到98总共要178+9=187位数;
(2)前面1到9位数,是1到9的和,后面接下来是10个1的和,再接下来是0到9的和,再接下来是10个2的和,再接下来是0到9的和,…,最后是10个9的和以及0到9的和,所以各个位上的数字之间和为10(1+2+3+4+5+6+7+8+9)+×2=900;
(3)根据两个数的和和两个数的差的奇偶性是相同的,所以若干次后剩余数的差和98个数的和的奇偶性相同,根据1、2、3、…98的和是(1+98)×98÷2=4851是奇数,4不是奇数,所以没有这种可能性.
解答 解:(1)9+(98-9)×2
=9+178
=187,
所以,这个新数是一个187位数;
(2)10(1+2+3+4+5+6+7+8+9)×2
=10×45×2
=900;
(3)由于两个数的和和两个数的差的奇偶性是相同的,
所以若干次后剩余数的差和98个数的和的奇偶性相同,
因为1+2+3+…+98=(1+98)×98÷2=4851是奇数,
4不是奇数,所以没有这种可能性.
点评 本题考查了学生对数的构成、对大数的认识以及分析能力;两个数的和和两个数的差的奇偶性是相同的是解(3)的关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 若两数相等,则它们的绝对值相等 | B. | 对顶角相等 | ||
| C. | 若a≥0,则${(\sqrt{a})}^{2}$=a | D. | 全等三角形面积相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
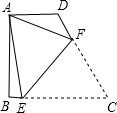 如图,在四边形ABCD中,AD∥BC,∠B=Rt∠,∠C=60°,AD=4,CD=8,点E在BC上,点F在CD上,现将四边形ABCD沿EF折叠,若点C洽与点A重合,EF为折痕,则CE=7,sin∠AFE=$\frac{5\sqrt{7}}{14}$.
如图,在四边形ABCD中,AD∥BC,∠B=Rt∠,∠C=60°,AD=4,CD=8,点E在BC上,点F在CD上,现将四边形ABCD沿EF折叠,若点C洽与点A重合,EF为折痕,则CE=7,sin∠AFE=$\frac{5\sqrt{7}}{14}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com