

分析 (1)根据等腰三角形性质求出即可,过点D作DM⊥EF于M,根据等腰直角三角形的性质求出ME=3,再表示出BM,然后根据△DBM和△ABC相似,利用相似三角形对应边成比例列式求解得到t;
(2)首先分类讨论,画出各种不同时间段的图形,计算各段函数关系式即可;
(3)①AP=AQ,求出即可;②AP=PQ,作PH⊥AC于H,根据相似得出比例式,即可求出答案;③AQ=PQ,作PH⊥AC于H,根据相似得出比例式,④当5≤t≤10时,AQ=PQ,作PH⊥BC,PG⊥AC,利用相似与勾股定理,即可求出答案
解答 解:(1)如图1,过点D作DM⊥EF于点M,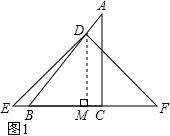
∵∠EDF=90°,∠DEF=45°,
∴△DEF是等腰直角三角形,
∵EF=10,
∴DM=EM=MF=5,
∵EC=t,
∴EB=t-6,
∴BM=6-(t-6)=12-t,
∵∠ACB=90°,DM⊥EF,
∴DM∥AC,
∴△DBM∽△ABC,
∴$\frac{BH}{BC}=\frac{DH}{AC}$,
∴$\frac{BH}{6}=\frac{5}{8}$,
解得:BH=$\frac{15}{4}$,
∴CH=6-$\frac{15}{4}$=$\frac{9}{4}$,t=5+$\frac{9}{4}$=$\frac{29}{4}$,
解得t=$\frac{29}{4}$;
当D在AC上时,
∵DE=DF,
∴EC=CF=$\frac{1}{2}$EF=5,
∴t=5.
(2)如图2,0≤t≤5时,S=$\frac{1}{2}$t2;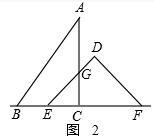
如图3,5<t≤6时,S=$\frac{1}{2}$•10•5-$\frac{1}{2}$•(10-t)2=$-\frac{1}{2}{t}^{2}+10t-25$;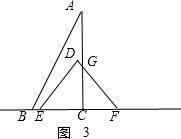
如图5,当点D落在AB上时,作DH⊥BC,DH=EH=5,PH∥AC,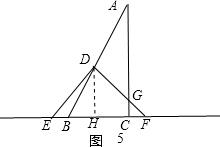
∴$\frac{BH}{BC}=\frac{DH}{AC}$,
∴$\frac{BH}{6}=\frac{5}{8}$,
解得:BH=$\frac{15}{4}$,
∴CH=6-$\frac{15}{4}$=$\frac{9}{4}$,CE=5+$\frac{9}{4}$=$\frac{29}{4}$,
∴如图4,当6<t≤$\frac{29}{4}$时,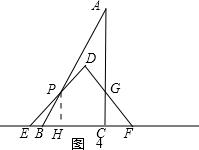
作PH⊥BC,则PH=EH,BH=EH-BE=PH-BE
∵PH∥AC
∴△BPH∽△BAC
∴$\frac{PH}{AC}=\frac{BH}{BC}$,
∴$\frac{PH}{8}=\frac{PH-(t-6)}{6}$,
∴PH=4t-24
∴S═$\frac{1}{2}$•10•5-$\frac{1}{2}$•(t-6)•(4t-24)-$\frac{1}{2}$•(10-t)2=-$\frac{5}{2}{t}^{2}+34t-97$;
如图6,当$\frac{29}{4}$<t≤10时,CH=t-5,AG=8-(10-t)=t-2,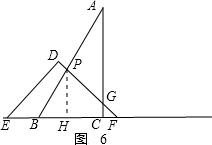
∴S=$\frac{1}{2}$•(t-1)•(t-5)=$\frac{1}{2}{t}^{2}+3t+\frac{5}{2}$;
(3)存在.
∵AP=t,∠EDF=90°,∠DEF=45°,
∴∠CQE=45°=∠DEF,
∴CQ=CE=t,
AQ=8-t,当0≤t<5时,
①AP=AQ,
t=8-t,
∴t=4;
②AP=PQ,
作PH⊥AC于H,如图7: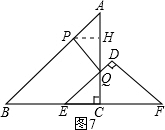
AH=HQ=$\frac{1}{2}$AQ=4-$\frac{1}{2}$t,
∵PH∥BC,
∴△APH∽△ABC,
∴$\frac{AP}{AH}$=$\frac{AB}{AC}$,
∴$\frac{t}{4-\frac{1}{2}t}$=$\frac{10}{8}$,
∴t=$\frac{40}{13}$;
③AQ=PQ,
作QI⊥AB于I,如图8: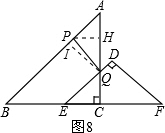
AI=PI=$\frac{1}{2}$AP=$\frac{1}{2}$t(等腰三角形的性质三线合一),
∵∠AIQ=∠ACB=90°,∠A=∠A,
∴△AIQ∽△ACB,
∴$\frac{AI}{AQ}$=$\frac{AC}{AB}$,
∴$\frac{\frac{1}{2}t}{8-t}$=$\frac{8}{10}$,
∴t=$\frac{64}{13}$,
④当5≤t≤10时,AQ=PQ,作PH⊥BC,PG⊥AC,如图9: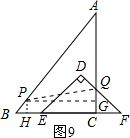
同理可求出,
FC=QC=10-t,BP=10-t,
PH=$\frac{4}{5}$(10-t)=8-$\frac{4}{5}$t,
BH=$\frac{3}{5}$(10-t)=6-$\frac{3}{5}$t,
QG=QC-GC=QC-PH=10-t-(8-$\frac{4}{5}$t)=2-$\frac{t}{5}$,
PG=HC=6-(6-$\frac{3}{5}$t)=$\frac{3}{5}$t,
PQ=AQ=8-(10-t)=t-2,
∴PQ 2=PG 2+QG 2,
(t-2)2=( $\frac{3}{5}$t) 2+(2-$\frac{t}{5}$) 2,
解得:t=$\frac{16}{3}$秒,
其它情况不符合要求.
综合上述:当t等于4秒、$\frac{40}{13}$秒、$\frac{64}{13}$秒、$\frac{16}{3}$秒时△APQ是等腰三角形.
点评 本题是相似形综合题,主要利用了等腰直角三角形的性质,相似三角形的判定与性质,三角形的面积,菱形的性质,难点在于(2)(3)两个小题要分情况讨论,作出图形更形象直观.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
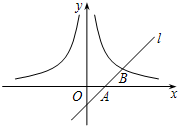 如图,已知直线l经过点A(1,0),与双曲线y=$\frac{m}{x}$(x>0)交于点B(2,1).过点P(p,p-1)(其中p>1)作 轴的平行线分别交双曲线y=$\frac{m}{x}$(x>0)和y=-$\frac{m}{x}$(x<0)于点M、N.
如图,已知直线l经过点A(1,0),与双曲线y=$\frac{m}{x}$(x>0)交于点B(2,1).过点P(p,p-1)(其中p>1)作 轴的平行线分别交双曲线y=$\frac{m}{x}$(x>0)和y=-$\frac{m}{x}$(x<0)于点M、N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
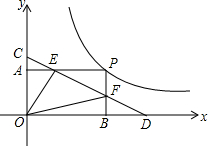 如图.矩形OAPB的顶点P在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点E、F分别是矩形的边PA,PB上的动点,直线EF分别交y轴、x轴于C,D两点.现给出如下命题:①若点E、F恰同在反比例函数y=$\frac{m}{x}$(k>m>0)的图象上,则S四边形OEPF=k-m;②△ACE≌△BFD;③若OC=OD=$\sqrt{2k}$,则△OCF∽△EOF;④CE+DF=EF.其中结论正确的是( )
如图.矩形OAPB的顶点P在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点E、F分别是矩形的边PA,PB上的动点,直线EF分别交y轴、x轴于C,D两点.现给出如下命题:①若点E、F恰同在反比例函数y=$\frac{m}{x}$(k>m>0)的图象上,则S四边形OEPF=k-m;②△ACE≌△BFD;③若OC=OD=$\sqrt{2k}$,则△OCF∽△EOF;④CE+DF=EF.其中结论正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
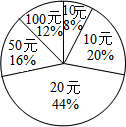 在一次捐款活动中,某班50名同学人人拿出自己的零花钱,有捐10元、20元和30元的,还有捐50元和100元的.如图反映了不同捐款数的人数比例,那么该班同学平均每人捐款31.2元.
在一次捐款活动中,某班50名同学人人拿出自己的零花钱,有捐10元、20元和30元的,还有捐50元和100元的.如图反映了不同捐款数的人数比例,那么该班同学平均每人捐款31.2元.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
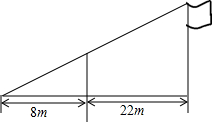 如图,小东用长3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )
如图,小东用长3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )| A. | 12m | B. | 10m | C. | 8m | D. | 7m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com