
分析 (1)原式通分并利用同分母分式的减法法则计算即可得到结果;
(2)原式第一项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=$\frac{x+1-2}{(x+1)(x-1)}$=$\frac{x-1}{(x+1)(x-1)}$=$\frac{1}{x+1}$;
(2)原式=$\frac{2(a+1)}{a-1}$•$\frac{1}{a+1}$-$\frac{(a+1)(a-1)}{(a-1)^{2}}$=$\frac{2}{a-1}$-$\frac{a+1}{a-1}$=$\frac{-(a-1)}{a-1}$=-1.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
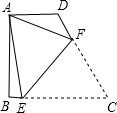 如图,在四边形ABCD中,AD∥BC,∠B=Rt∠,∠C=60°,AD=4,CD=8,点E在BC上,点F在CD上,现将四边形ABCD沿EF折叠,若点C洽与点A重合,EF为折痕,则CE=7,sin∠AFE=$\frac{5\sqrt{7}}{14}$.
如图,在四边形ABCD中,AD∥BC,∠B=Rt∠,∠C=60°,AD=4,CD=8,点E在BC上,点F在CD上,现将四边形ABCD沿EF折叠,若点C洽与点A重合,EF为折痕,则CE=7,sin∠AFE=$\frac{5\sqrt{7}}{14}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com