
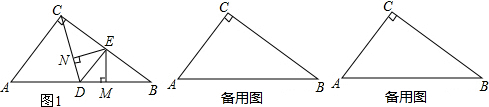
分析 (1)由等腰三角形的性质得出∠DAC=∠DCA,由三角形的外角性质和角平分线得出得出∠DAC=∠BDE,即可得出结论;
(2)分两种情况:①当△BME∽△CNE时,得出对应角相等∠MBE=∠NCE,得出BD=CD=AD,证出DE∥AC,得出$\frac{1}{2}$=$\frac{BD}{AB}$,由勾股定理求出AB,得出BD,即可得出AD;②当△BME∽△ENC时,得出∠EBM=∠CEN,由勾股定理求出AB,由由三角形面积求出CD=$\frac{AC•BC}{AB}$=$\frac{6×8}{10}$=$\frac{24}{5}$,由勾股定理求出AD即可;
(3)由AAS证明△MDE≌△DEN,得出S△MDE=S△DEN=$\frac{1}{2}$DM•ME,证出EM是BD的垂直平分线,得出∠EDB=∠DBE,证明△CDE∽△CBD,得出对应边成比例,CE=$\frac{C{D}^{2}}{BC}$,求出CD=$\frac{4BE}{BM}$,由三角函数得出$\frac{BE}{BM}$=$\frac{5}{4}$,求出CD、CE,得出BE,由三角函数求出BM,即可得出AD.
解答 (1)证明:∵AD=CD,
∴∠DAC=∠DCA,
∴∠CDB=∠DAC+∠DCA=2∠DAC,
又∵DE是∠CDB的平分线,
∴∠CDB=2∠BDE,
∴∠DAC=∠BDE,
∴DE∥AC;
(2)解:①如图1所示: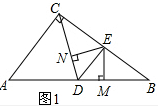
当△BME∽△CNE时,
得∠MBE=∠NCE,
∴BD=CD=AD,
∵DE平分∠BDC,
∴DE⊥BC,BE=EC,BE=$\frac{1}{2}$BC,
又∵∠ACB=90°,
∴DE∥AC,
∴$\frac{BE}{BC}=\frac{BD}{AB}$,
即$\frac{1}{2}$=$\frac{BD}{AB}$,
∴BD=$\frac{1}{2}$AB=$\frac{1}{2}$$\sqrt{A{C}^{2}+B{C}^{2}}$=$\frac{1}{2}$$\sqrt{{6}^{2}+{8}^{2}}$=5,
∴AD=5;
②如图2所示: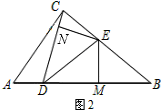 当△BME∽△ENC时,
当△BME∽△ENC时,
得∠EBM=∠CEN,
∴EN∥BD,
又∵EN⊥CD,
∴BD⊥CD,
即CD是△ABC斜边上的高,
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
由三角形面积公式得:AB•CD=AC•BC,
∴CD=$\frac{AC•BC}{AB}$=$\frac{6×8}{10}$=$\frac{24}{5}$,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{{6}^{2}-(\frac{24}{5})^{2}}$=$\frac{18}{5}$;
综上所述,当AD=5或$\frac{18}{5}$时,△BME与△CNE相似.
(3)解:∵DE是∠CDB的平分线,
∴∠MDE=∠NDE,
在△MDE和△DEN中,$\left\{\begin{array}{l}{∠MDE=∠NDE}\\{∠DME=∠DNE=90°}\\{DE=DE}\end{array}\right.$,
∴△MDE≌△DEN(AAS),
∴S△MDE=S△DEN=$\frac{1}{2}$DM•ME,
∵S四边形MEND=S△BDE,
∴2×$\frac{1}{2}$DM•ME=$\frac{1}{2}$BD•ME,
即DM=$\frac{1}{2}$BD,
∴EM是BD的垂直平分线,
∴∠EDB=∠DBE,
∵∠EDB=∠CDE,
∴∠DBE=∠CDE,
又∵∠DCE=∠BCD,
∴△CDE∽△CBD,
∴$\frac{CD}{BC}$=$\frac{CE}{CD}$=$\frac{DE}{BD}$,
即CE=$\frac{C{D}^{2}}{BC}$,
∴$\frac{CD}{BC}=\frac{BE}{BD}=\frac{BE}{2BM}$,
∵BC=8,
即CD=$\frac{4BE}{BM}$,
∵cos∠B=$\frac{BM}{BE}$=$\frac{BC}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$,
∴$\frac{BE}{BM}$=$\frac{5}{4}$,
∴CD=4×$\frac{5}{4}$=5,CE=$\frac{C{D}^{2}}{BC}$=$\frac{{5}^{2}}{8}$=$\frac{25}{8}$,
∴BE=8-$\frac{25}{8}$=$\frac{39}{8}$,
∴BM=cos∠B•BE=$\frac{4}{5}$×$\frac{39}{8}$=$\frac{39}{10}$,
∴AD=AB-2BM=10-2×$\frac{39}{10}$=$\frac{11}{5}$.
点评 本题是四边形综合题目,考查了平行线的判定、相似三角形的判定与性质、勾股定理、全等三角形的判定与性质、三角函数等知识;本题综合性强,难度较大,特别是(2)中,需要进行分类讨论才能得出结果.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344\end{array}$ | B. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344+306\end{array}$ | ||
| C. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344-306\end{array}$ | D. | $\left\{\begin{array}{l}344y=306x\\ 65(x-y)=344+306\end{array}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=2,y=3 | B. | x=3,y=-1 | C. | x=2,y=-3 | D. | x=3,y=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若两数相等,则它们的绝对值相等 | B. | 对顶角相等 | ||
| C. | 若a≥0,则${(\sqrt{a})}^{2}$=a | D. | 全等三角形面积相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com