
分析 ①先把各二次根式化为最简二次根式,然后合并即可;
②根据二次根式的乘法法则运算;
③先分母有理化,然后进行二次根式的乘法运算;
④利用平方差公式和完全平方公式计算;
⑤先把各二次根式化为最简二次根式,然后合并即可.
解答 解:①原式=2$\sqrt{2}$+2$\sqrt{3}$-3$\sqrt{2}$
=2$\sqrt{3}$-$\sqrt{2}$;
②原式=$\sqrt{6×3}$+$\sqrt{8×3}$
=3$\sqrt{2}$+2$\sqrt{6}$;
③原式=2$\sqrt{3}$($\sqrt{3}$+$\sqrt{2}$)
=6+2$\sqrt{6}$;
④原式=1-(2$\sqrt{3}$)2-(12-4$\sqrt{3}$+1)
=1-12-13+4$\sqrt{3}$
=-24+4$\sqrt{3}$;
⑤原式=4$\sqrt{3}$-$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$
=3$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
| 数量x(千克) | 1 | 2 | 3 | 4 | … |
| 售价y(元) | 8+0.4 | 16+0.8 | 24+1.2 | 32+1.6 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
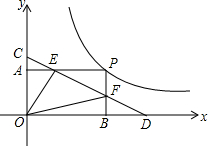 如图.矩形OAPB的顶点P在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点E、F分别是矩形的边PA,PB上的动点,直线EF分别交y轴、x轴于C,D两点.现给出如下命题:①若点E、F恰同在反比例函数y=$\frac{m}{x}$(k>m>0)的图象上,则S四边形OEPF=k-m;②△ACE≌△BFD;③若OC=OD=$\sqrt{2k}$,则△OCF∽△EOF;④CE+DF=EF.其中结论正确的是( )
如图.矩形OAPB的顶点P在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点E、F分别是矩形的边PA,PB上的动点,直线EF分别交y轴、x轴于C,D两点.现给出如下命题:①若点E、F恰同在反比例函数y=$\frac{m}{x}$(k>m>0)的图象上,则S四边形OEPF=k-m;②△ACE≌△BFD;③若OC=OD=$\sqrt{2k}$,则△OCF∽△EOF;④CE+DF=EF.其中结论正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com