
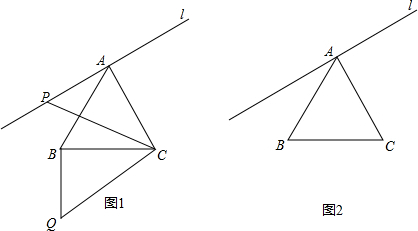
���� ��1��������ת�����ʵõ���QBC=��PAC=90�㣻
��2���������⻭��ͼ�Σ����ù��ɶ������m��ֵ��
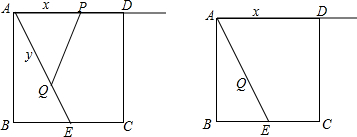
��3����BG��AC�ڵ�G������Q��ֱ��l�Ĵ��߽�l�ڵ�D����BG�ڵ�F����֤�ı���ADFGΪ���Σ��ɵȱߡ�ABC����������֪DF=$\frac{1}{2}$AC=2����CBG=$\frac{1}{2}$��CBA=30�㣻������ת�����ʵõ�����ACP�ա�BCQ�������Ӧ����ȣ�AP=BQ=m����Ӧ����ȡ�PAC=��QBC=90�㣬����ͨ����Rt��QBF���QF=$\frac{\sqrt{3}}{2}$m��Ҫʹ��PAQ���ڣ����P�������A��P1�غϣ����Ե�P��λ�÷�Ϊ�������������
i����ͼ2������P�ڣ�2���е��߶�P1A�ϣ���P�����A��P1�غϣ�ʱ���ɵ�0��m��$\frac{4\sqrt{3}}{3}$����ʱ��Q��ֱ��l���·����������ε������ʽ����m��ֵ��
ii����ͼ3������P�ڣ�2���е��߶�AP1���ӳ����ϣ���P�����A��P1�غϣ�ʱ���ɵ�m��$\frac{4\sqrt{3}}{3}$����ʱ��Q��ֱ��l���Ϸ����������ε������ʽ����m��ֵ��
��� 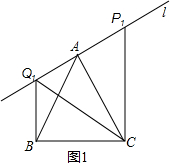 �⣺��1���١�AC��l��
�⣺��1���١�AC��l��
���PAC=90�㣬
������ת�����ʵõ�����QBC=��PAC=90�㣮
��m=3ʱ����Q��ֱ��l�ľ������2+$\frac{3\sqrt{3}}{2}$��
�ʴ��ǣ�90��2+$\frac{3\sqrt{3}}{2}$��
��2������ͼ�μ�ͼ1��m=$\frac{4\sqrt{3}}{3}$��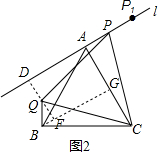
��3����ͼ2����BG��AC�ڵ�G������Q��ֱ��l�Ĵ��߽�l�ڵ�D����BG�ڵ�F��
��CA��ֱ��l��
���CAP=90�㣮
��֤�ı���ADFGΪ���Σ�
�ߵȱ�������ABC�ı߳�Ϊ4��
���ACB=60�㣬DF=AG=CG=$\frac{1}{2}$AC=2����CBG=$\frac{1}{2}$��CBA=30�㣮
�߽���ACP�Ƶ�C����ʱ�뷽����ת60��õ���BCQ��
���ACP�ա�BCQ��
��AP=BQ=m����PAC=��QBC=90�㣮
���QBF=60�㣮
��Rt��QBF�У���QFB=90�㣬��QBF=60�㣬BQ=m��
��QF=$\frac{\sqrt{3}}{2}$m��
Ҫʹ��PAQ���ڣ����P�������A��P1�غϣ����Ե�P��λ�÷�Ϊ�������������
i����ͼ2������P�ڣ�2���е��߶�P1A�ϣ���P�����A��P1�غϣ�ʱ���ɵ�0��m��$\frac{4\sqrt{3}}{3}$��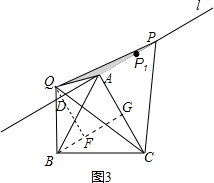 ��ʱ��Q��ֱ��l���·���
��ʱ��Q��ֱ��l���·���
��DQ=DF-QF=2-$\frac{\sqrt{3}}{2}$m��
��S��PAQ=$\frac{1}{2}$AP•DQ=$\frac{\sqrt{3}}{4}$��
��$\frac{1}{2}$m��2-$\frac{\sqrt{3}}{2}$m��=$\frac{\sqrt{3}}{4}$��
��������$\sqrt{3}$m2-4m+$\sqrt{3}$=0��
���m1=$\frac{\sqrt{3}}{3}$��m2=$\sqrt{3}$��
�����飬m=$\frac{\sqrt{3}}{3}$��$\sqrt{3}$��0��m��$\frac{4\sqrt{3}}{3}$�ķ�Χ�ڣ����������⣮
ii����ͼ3������P�ڣ�2���е��߶�AP1���ӳ����ϣ���P�����A��P1�غϣ�ʱ���ɵ�m��$\frac{4\sqrt{3}}{3}$����ʱ��Q��ֱ��l���Ϸ���
��DQ=QF-DF=$\frac{\sqrt{3}}{2}$m-2��
��S��PAQ=$\frac{1}{2}$AP•DQ=$\frac{\sqrt{3}}{4}$��
��$\frac{1}{2}$m��$\frac{\sqrt{3}}{2}$m-2��=$\frac{\sqrt{3}}{4}$��
�������� 3m2-4$\sqrt{3}$m-3=0��
��� m=$\frac{2\sqrt{3}��\sqrt{21}}{3}$���Ḻ����
�����飬m=$\frac{2\sqrt{3}+\sqrt{21}}{3}$��m��$\frac{4\sqrt{3}}{3}$�ķ�Χ�ڣ��������⣮
����������m=$\frac{\sqrt{3}}{3}$��$\sqrt{3}$��$\frac{2\sqrt{3}+\sqrt{21}}{3}$ʱ����PAQ���������$\frac{\sqrt{3}}{4}$��
���� ������Ҫ�����˼���֪ʶ���ۺ����úͼ��α任��������߶εij��Ⱥͽ�һԪ���η��������ô�����������������⣬�������ڼ�ǿѧ����ͼ���뼸�ε��������Լ����������ۺ�������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=2��y=3 | B�� | x=3��y=-1 | C�� | x=2��y=-3 | D�� | x=3��y=-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
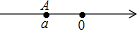 ��ͼ�������ϵĵ�A����ʾ��������a=-2���������ϵĵ�B���A֮��ľ�����5�����B����ʾ��������b=-7��3��
��ͼ�������ϵĵ�A����ʾ��������a=-2���������ϵĵ�B���A֮��ľ�����5�����B����ʾ��������b=-7��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a��b��b��c����a��c | B�� | ��a��b��b��c����a��c | C�� | ��a��c��b��c����a��b | D�� | ��a��c��b��a����b��c |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com