
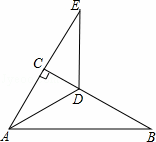
�ھ���ABCD�У�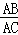 =a����G��H�ֱ��ڱ�AB��DC�ϣ���HA=HG����EΪAB���ϵ�һ�����㣬����HE���ѡ�AHE��ֱ��HE���۵õ���FHE��
=a����G��H�ֱ��ڱ�AB��DC�ϣ���HA=HG����EΪAB���ϵ�һ�����㣬����HE���ѡ�AHE��ֱ��HE���۵õ���FHE��
��1����ͼ1����DH=DAʱ��
����գ���HGA=��45���ȣ�
����EF��HG�����AHE�Ķ����������ʱ����Сֵ��
��2����ͼ3����AEH=60�㣬EG=2BG������FG������FG������DC�ڵ�P����FG��AB��GΪ���㣬��a��ֵ��
�⣺��1���١��ı���ABCD�Ǿ��Σ�
���ADH=90�㣬
��DH=DA��
���DAH=��DHA=45�㣬
���HAE=45�㣬
��HA=HG��
���HAE=��HGA=45�㣻
�ʴ�Ϊ��45�㣻
�ڷ�����������ۣ�
��һ�������
�ߡ�HAG=��HGA=45�㣻
���AHG=90�㣬
���۵���֪����HAE=��F=45�㣬��AHE=��FHE��
��EF��HG��
���FHG=��F=45�㣬
���AHF=��AHG﹣��FHG=45�㣬
����AHE+��FHE=45�㣬
���AHE=22.5�㣬
��ʱ����B��G�غ�ʱ��a��ֵ��С����Сֵ��2��
�ڶ��������
��EF��HG��
���HGA=��FEA=45�㣬
����AEH+��FEH=45�㣬
���۵���֪����AEH=��FEH��
���AEH=��FEH=22.5�㣬
��EF��HG��
���GHE=��FEH=22.5�㣬
���AHE=90��+22.5��=112.5�㣬
��ʱ����B��E�غ�ʱ��a��ֵ��С��
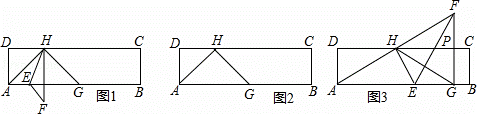
��DH=DA=x����AH=CH=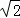 x��
x��
��Rt��AHG�У���AHG=90�㣬�ɹ��ɶ����ã�
AG=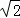 AH=2x��
AH=2x��
�ߡ�AEH=��FEH����GHE=��FEH��
 ���AEH=��GHE��
���AEH=��GHE��
��GH=GE=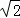 x��
x��
��AB=AE=2x+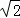 x��
x��
��a����Сֵ��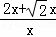 =2+
=2+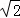 ��
��
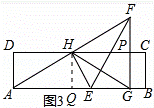
��2����ͼ������H��HQ��AB��Q�����AQH=��GOH=90�㣬
�ھ���ABCD�У���D=��DAQ=90�㣬
���D=��DAQ=��AQH=90�㣬
���ı���DAQHΪ���Σ�
��AD=HQ��
��AD=x��GB=y����HQ=x��EG=2y��
���۵���֪����AEH=��FEH=60�㣬
���FEG=60�㣬
��Rt��EFG�У�EG=EF��cos60�㣬EF=4y��
��Rt��HQE��EQ=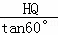 =
=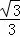 x��
x��
��QG=QE+EG=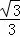 x+2y��
x+2y��
��HA=HG��HQ��AB��
��AQ=GQ=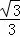 x+2y��
x+2y��
��AE=AQ+QE=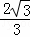 x+2y��
x+2y��
���۵���֪��AE=EF��
��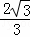 x+2y=4y��
x+2y=4y��
��y=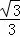 x��
x��
��AB=2AQ+GB=2��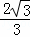 x+2y��+y=
x+2y��+y= x��
x��
��a=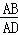 =
= ��
��


 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�����������εĶ���Ϊ40�㣬�����ĵǶ���Ϊ��������
�� A�� 40�� B�� 50�� C�� 60�� D�� 70��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
Ҫʹ��ʽ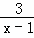 �����壬���ȡֵ��Χ�ǣ�������
�����壬���ȡֵ��Χ�ǣ�������
| �� | A�� | x��1 | B�� | x��1 | C�� | x��1 | D�� | x��﹣1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����Rt��ABC�У���ACB=90�㣬��B=30�㣬ADƽ�֡�CAB��
��1�����CAD�Ķ�����
��2���ӳ�AC��E��ʹCE=AC����֤��DA=DE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����4����ͬ��С�����δ�ɵ�һ�������壬�����ĸ���ͼ�ǣ�������

| �� | A�� |
| B�� |
| C�� |
| D�� |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�����������ABCDE�У�����AC��AD��CE��CE��AD�ڵ�F������BF������˵������ȷ���ǣ�������

| �� | A�� | ��CDF���ܳ�����AD+CD | B�� | FCƽ�֡�BFD |
| �� | C�� | AC2+BF2=4CD2 | D�� | DE2=EF•CE |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����˵����ȷ���ǣ�������
| �� | A�� | �����ӻ��������ڲ���桱�DZ�Ȼ�¼� |
| �� | B�� | ��һ�������Ĵ���װ��8������������һ�����Ǻ���������¼� |
| �� | C�� | Ϊ���˽����н����ļ��ҵ��г��пյ������������˲����ղ�ĵ��鷽ʽ���� |
| �� | D�� | ����ij��Ʒ�Ƶ���Ь�������������Ȥ���Ǹ�Ʒ����Ь�ij����ƽ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com