
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.

【答案】(1)详见解析;(2)75°
【解析】
①求出∠ABE=∠CBD,然后利用“边角边”证明△ABE和△CBD全等即可;
②先根据等腰直角三角形的锐角都是45°求出∠CAB,再求出∠BAE,然后根据全等三角形对应角相等求出∠BCD,再根据直角三角形两锐角互余其解即可;
①证明:∵∠ABC=90°,D为AB延长线上一点,
∴∠ABE=∠CBD=90°,
在△ABE和△CBD中,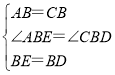 ,
,
∴△ABE≌△CBD(SAS);
②∵AB=CB,∠ABC=90°,
∴∠CAB=45°,
∵∠CAE=30°,
∴∠BAE=∠CAB-∠CAE=45°-30°=15°,
∵△ABE≌△CBD,
∴∠BCD=∠BAE=15°,
∴∠BDC=90°-∠BCD=90°-15°=75°;


科目:初中数学 来源: 题型:
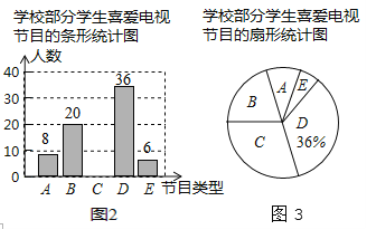
【题目】为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,课题小组随机选取该校部分学生进行了问卷调査(问卷调査表如图1所示),并根据调查结果绘制了图2、图3两幅统计图(均不完整),请根据统计图解答下列问题.
(1)本次接受问卷调查的学生有________名.
(2)补全条形统计图.
(3)扇形统计图中B类节目对应扇形的圆心角的度数为________.
(4)该校共有2000名学生,根据调查结果估计该校最喜爱新闻节目的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是由
是由![]() 经过平移得到的,其中A,B,C三点的对应点分别是
经过平移得到的,其中A,B,C三点的对应点分别是![]() ,
,![]() ,
,![]() ,它们在平面直角坐标系中的坐标如下表所示:
,它们在平面直角坐标系中的坐标如下表所示:
|
|
|
|
|
|
|
|
(1)观察表中各对应点坐标的变化,并填空:![]() __________,
__________,![]() __________.
__________.
(2)在下图的平面直角坐标系中画出![]() 和
和![]() .
.
(3)写出![]() 是怎样平移得到
是怎样平移得到![]() 的?
的?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3),B(﹣3,1),C(﹣1,3).
(1)请按下列要求画图:
①平移△ABC,使点A的对应点A1的坐标为(﹣4,﹣3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2.
(2)若将△A1B1C1绕点M旋转可得到△A2B2C2,请直接写出旋转中心M点的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线![]() .下列结论中,正确的是( )
.下列结论中,正确的是( )

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
查看答案和解析>>
科目:初中数学 来源: 题型:
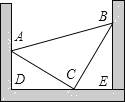
【题目】如图,一个等腰直角三角形零件放置在一凹槽内,顶点A.B.C分别落在凹槽内壁上,测得AD=5cm,BE=9cm,则该零件的面积为 _______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com