
【题目】已知:如图,△ABC中,∠C=90°,CM⊥AB于M,AT平分∠BAC交CM于D,交BC于T,过D作DE∥AB交BC于E,求证CT=BE
.
【答案】见解析
【解析】
过T作TF⊥AB于F,根据角平分线上的点到角的两边的距离相等得TF=CT,再根据角平分线的定义和等角的余角相等的性质得到∠CDT=∠CTD,所以CD=CT,再证明△CDE和△TFB全等,然后根据全等三角形对应边相等可以得到CE=TB,都减去TE即可得到CT=BE.
证明:过T作TF⊥AB于F,
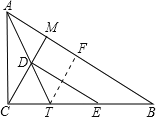
∵AT平分∠BAC,∠ACB=90°,
∴CT=TF(角平分线上的点到角两边的距离相等),
∵∠ACB=90°,CM⊥AB,
∴∠ADM+∠DAM=90°,∠ATC+∠CAT=90°,
∵AT平分∠BAC,
∴∠DAM=∠CAT,
∴∠ADM=∠ATC,
∴∠CDT=∠CTD,
∴CD=CT,
又∵CT=TF(已证),
∴CD=TF,
∵CM⊥AB,DE∥AB,
∴∠CDE=90°,∠B=∠DEC,
在△CDE和△TFB中,
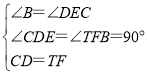 ,
,
∴△CDE≌△TFB(AAS),
∴CE=TB,
∴CE-TE=TB-TE,
即CT=BE.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC⊥BD,且AC=8,BD=4,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为( )
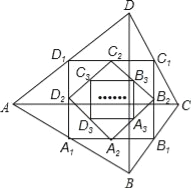
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点A到航线![]() 的距离为2km,点B位于点A北偏东60°方向且与A相距10km.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5分钟后该轮船行至点A的正北方向的D处.
的距离为2km,点B位于点A北偏东60°方向且与A相距10km.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5分钟后该轮船行至点A的正北方向的D处.
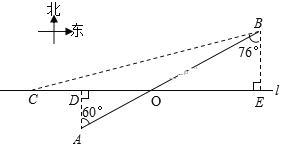
(1)求观测点B到航线![]() 的距离;
的距离;
(2)求该轮船航行的速度(结果精确到0.1km/h).
(参考数据: ![]() ≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=2x+8的图象分别交x轴、y轴于A、B两点,过点A的直线交y轴正半轴于点M,且点M为线段OB的中点.

(1)求直线AM的函数解析式.
(2)试在直线AM上找一点P,使得S△ABP=S△AOB,求出点P的坐标.
(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、B、M、H为顶点的四边形是平行四边形?若存在,请直接写出所有点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=x2+bx-1的图象经过点(2,3).
(1)求这个函数的表达式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)观察图象,说明y随x的增大是怎样变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两人骑自行车绕800米圆形跑道行驶,他们从同一地点出发,如果方向相反,每一分二十秒相遇一次,如果方向相同,每十三分二十秒相遇一次.假设二人速度不等,求各人速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com