
 |
| AB |
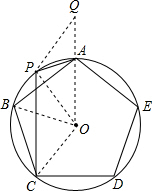 证明:连接OA并延长至Q,使得AQ=PA;连接OP、OC、OB.
证明:连接OA并延长至Q,使得AQ=PA;连接OP、OC、OB.| 360° |
| 5 |
 |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
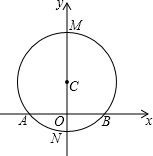 如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标
如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
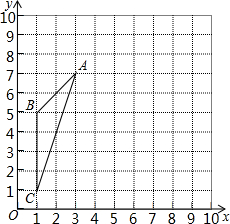 如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com