
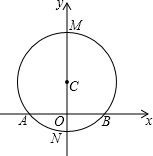
 如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标
如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标| 1 |
| 2 |
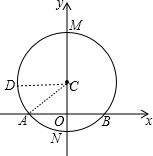 连结AC,如图,作半径CD⊥y轴,
连结AC,如图,作半径CD⊥y轴,| 1 |
| 2 |
| AC2-AO2 |
| 6 |
| 6 |
| 21 |
| 21 |


科目:初中数学 来源: 题型:
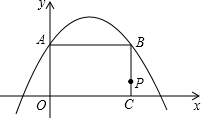 如图,已知二次函数y=-
如图,已知二次函数y=-| 1 |
| 6 |
| 1 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD是一个长方形的台球桌,台球桌上还剩一个黑球没有被打进球袋,在点P的位置,现在轮到你打,你应该把在点Q位置的白球打到AB边上的哪一个点,才能反弹回来撞到黑球?试作图说明.
如图,四边形ABCD是一个长方形的台球桌,台球桌上还剩一个黑球没有被打进球袋,在点P的位置,现在轮到你打,你应该把在点Q位置的白球打到AB边上的哪一个点,才能反弹回来撞到黑球?试作图说明.查看答案和解析>>
科目:初中数学 来源: 题型:
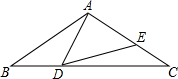 如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:
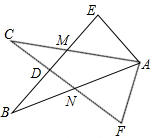 如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是
如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com