
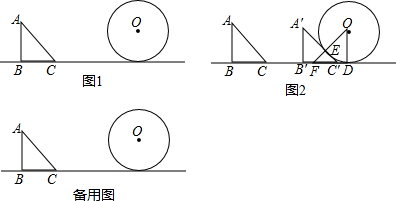
分析 (1)①直接利用圆心O与直线AB的距离为5,以及⊙O的半径为1和△ABC移动的速度求出答案;
②第一次相切时,与斜边相切,假设此时,△ABC移至△A′B′C′处,A′C′与⊙O切于点D,连OD并延长,交B′C′于F.由切线长定理易得CC′的长,进而由三角形运动的速度可得答案;
(2)①△ABC与⊙O从开始运动到最后一次相切时,应为AB与圆相切,路程差为6,速度差为1,故从开始运动到最后一次相切的时间为6秒;
②求出⊙O与△A′B′C′第二次相切时运动的时间,连接B′′O并延长交A′′C′′于点P,则B′′P⊥A′′C′′,求出OP的长即可得出结论.
解答 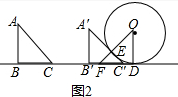 解:(1)①∵⊙O的半径为1,圆心O与直线AB的距离为5,现△ABC以每秒2个单位的速度向右移动,
解:(1)①∵⊙O的半径为1,圆心O与直线AB的距离为5,现△ABC以每秒2个单位的速度向右移动,
∴当移动$\frac{5}{2}$=2.5(秒),或$\frac{7}{2}$=3.5(秒)时,边AB所在的直线与⊙O相切.
故答案为:2.5秒或3.5;
②如图2,由题意可得:C′D=C′E=x,∠A′C′B′=45°,∠OEC′=90°,
则∠OFD=45°,故EF=EC′=x,
则FC′=$\sqrt{2}$x,
∵DO=DF=1,
∴x+$\sqrt{2}$x=1,
解得:x=$\sqrt{2}$-1,
则点B移动的距离为:BB′=CC′=BD-BC-DC′=5-1-($\sqrt{2}$-1)=5-$\sqrt{2}$.
故答案为:$\sqrt{2}$x;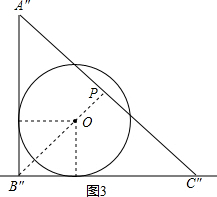
(2)①设一共经过了t秒,根据题意得:2t-5=t+1,
解得:t=6.
则△ABC从开始移动,到它的边与圆最后一次相切,一共经过6秒;
②∵△ABC与⊙O从开始运动到第二次相切时,2t+1=t+5,
解得t=4,
∴从开始运动到第二次相切的时间为4秒,此时△ABC移至△A′′B′′C′′处,A′′B′′=1+4×$\frac{1}{2}$=3
如图3,连接B′′O并延长交A′′C′′于点P,则B′′P⊥A′′C′′,且OP=$\frac{3\sqrt{2}}{2}$-$\sqrt{2}$=$\frac{\sqrt{2}}{2}$<1,
∴此时⊙O与A′′C′′相交,
∴不存在△ABC各边与⊙O都相切.
点评 本题考查的是圆的综合题,涉及的知识有:圆与直线的位置关系、切线长定理、切线的性质、平移的性质以及等腰直角三角形的性质,利用了数形结合的思想,利用数形结合再利用方程求出是解题关键.


科目:初中数学 来源: 题型:填空题
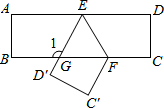 如图,将一张长方形纸片ABCD沿EF折叠,ED′与BC交于点为G,点D、点C分别落在点D′、点C′的位置上,若∠EFG=58°,则∠1=116°.
如图,将一张长方形纸片ABCD沿EF折叠,ED′与BC交于点为G,点D、点C分别落在点D′、点C′的位置上,若∠EFG=58°,则∠1=116°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60 | B. | 80 | C. | 3×220 | D. | 10×220 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若|a-b|=0,则a=b | |
| B. | 等式||m|+1|=|m|+1 | |
| C. | 若|-x|=|-7|,则x=±7 | |
| D. | 对一切有理数p,都一定有等式|-p|=p成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com