
【题目】观察下面三行数
3,9,27,81…①
1,3,9,27…②
2,10,26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③ 行的2019个数,求![]() 的值
的值
【答案】(1)(-3)1,(-3)2,(-3)3,(-3)4,…(-3)n;(2)第②行数是第①行数相应的数的-![]() ,第③行数的比第①行的数大1;(3)1.
,第③行数的比第①行的数大1;(3)1.
【解析】
(1)观察可看出第一行的数分别是-3的1次方,二次方,三次方,四次方…且偶数项是正数,奇数项是负数,用式子表示规律为:(-3)n;
(2)观察②,③两行的数与第①行的联系,即可得出答案;
(3)分别求得第①②③行的2019个数,得出x,y,z代入求得答案即可.
解:(1)∵-3,9,-27,81,-243,729…;
∴第①行数是:(-3)1,(-3)2,(-3)3,(-3)4,…(-3)n;
(2)第②行数是第①行数相应的数的![]() 即-
即-![]() ×(-3)n,
×(-3)n,
第③行数的比第①行的数大1即(-3)n+1;
(3)∵x=-32019,y=-![]() ×(-3)2019=32018,z=-32019+1,
×(-3)2019=32018,z=-32019+1,
∴x+6y+z=-32019+6×32018+(-32019+1)=1.


科目:初中数学 来源: 题型:
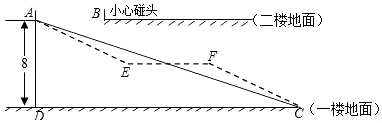
【题目】某大型购物商场在一楼和二楼之间安装自动扶梯AC,截面如图所示,一楼和二楼地面平行(即AB所在的直线与CD平行),层高AD为8米,∠ACD=20°,为使得顾客乘坐自动扶梯时不至于碰头,A、B之间必须达到一定的距离.
(1)要使身高2.26米的姚明乘坐自动扶梯时不碰头,那么A、B之间的距离至少要多少米?(精确到0.1米)
(2)如果自动扶梯改为由AE、EF、FC三段组成(如图中虚线所示),中间段EF为平台(即EF∥DC),AE段和FC段的坡度i=1:2,求平台EF的长度.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
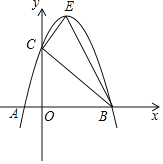
【题目】如图,已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,点C为抛物线与y轴的交点.
,点C为抛物线与y轴的交点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点E为直线BC上方抛物线上的一点,请求出
若点E为直线BC上方抛物线上的一点,请求出![]() 面积的最大值.
面积的最大值.
![]() 在
在![]() 条件下,是否存在这样的点
条件下,是否存在这样的点![]() ,使得
,使得![]() 为等腰三角形?如果有,请直接写出点D的坐标;如果没有,请说明理由.
为等腰三角形?如果有,请直接写出点D的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
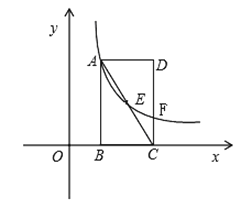
【题目】如图, 在直角坐标系中,长方形ABCD的边BC在X轴上,点B、D的坐标分别为B(1,0),D(3,3).
(1)直接写出点A、点C的坐标:A: C: ;
(2)若反比例函数![]() 的图象经过直线AC上的点E,且点E的坐标为(2,m),求
的图象经过直线AC上的点E,且点E的坐标为(2,m),求![]() 的值及反比例函数的解析式;
的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接 EF,在线段AB上(端点除外)找一点P,使得:S△PEF=S△cEF,并求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:求若干个相同的有理数(均不等于 0)的除法运算叫做除方,如 2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈 3 次方,”(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作:“(﹣3)的圈 4 次方”.一般地,把![]() 个记作 a,读作 “a 的圈 n次方”
个记作 a,读作 “a 的圈 n次方”
(初步探究)
(1)直接写出计算结果:2③,(﹣![]() )③.
)③.
(深入思考)
2③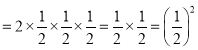
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(2)试一试,仿照上面的算式,将下列运算结果直接写成幂的形式.5⑥;(﹣![]() )⑩.
)⑩.
(3)猜想:有理数 a(a≠0)的圈n(n≥3)次方写成幂的形式等于多少.
(4)应用:求(-3)8×(-3)⑨-(﹣![]() )9×(﹣
)9×(﹣![]() )⑧
)⑧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列各题中![]() 关于
关于![]() 的函数关系式,并判断
的函数关系式,并判断![]() 是否为
是否为![]() 的一次函数,是否为正比例函数.
的一次函数,是否为正比例函数.
(1)长方形的面积为20,长方形的长![]() 与宽
与宽![]() 之间的函数关系式;
之间的函数关系式;
(2)刚上市时西瓜每千克3.6元,买西瓜的总价![]() 元与所买西瓜
元与所买西瓜![]() 千克之间的函数关系式;
千克之间的函数关系式;
(3)仓库内有粉笔400盒,如果每个星期领出36盒,仓库内余下的粉笔盒数![]() 与星期数
与星期数![]() 之间的函数关系式;
之间的函数关系式;
(4)爸爸为小林存了一份教育储蓄,首次存入10 000元,以后每个月存入500元,存入总数![]() 元与月数
元与月数![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
将几何图形按照某种法则或规则变换成另一种几何图形的过程叫做几何变换.旋转变换是几何变换的一种基本模型.经过旋转,往往能使图形的几何性质明白显现.题设和结论中的元素由分散变为集中,相互之间的关系清楚明了,从而将求解问题灵活转化.
问题提出:如图1,![]() 是边长为1的等边三角形,
是边长为1的等边三角形,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() ,求
,求![]() 的最小值.
的最小值.
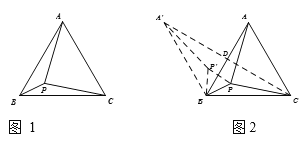
方法通过转化,把由三角形内一点发出的三条线段(星型线)转化为两定点之间的折线(化星为折),再利用“两点之间线段最短”求最小值(化折为直).
问题解决:如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() 、
、![]() ,记
,记![]() 与
与![]() 交于点
交于点![]() ,易知
,易知![]() ,
,![]() .由
.由![]() ,
,![]() ,可知
,可知![]() 为正三角形,有
为正三角形,有![]() .
.
故![]() .因此,当
.因此,当![]() 共线时,
共线时,![]() 有最小值是
有最小值是![]() .
.
学以致用:(1)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() 、
、![]() ,则
,则![]() 的最小值是__________.
的最小值是__________.
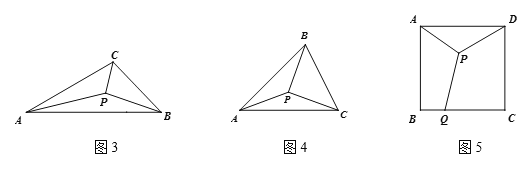
(2)如图4,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
(3)如图5,![]() 是边长为2的正方形
是边长为2的正方形![]() 内一点,
内一点,![]() 为边
为边![]() 上一点,连接
上一点,连接![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com