Question

5．如图，已知开口向上的抛物线与x轴分别交于点A（m，0）和B（-3m，0）（其中m＜0），与y轴交于点C（0，-3），点D在该抛物线上，CD∥AB．
（1）当m=-1时，求该抛物线所表示的函数关系式；
（2）在线段AB上是否存在点E，使得线段ED，BC互相垂直平分？若存在，求出点E的坐标，若不存在，请说明理由；
（3）设抛物线的顶点为F，作直线CF交x轴于点G，求证：$\frac{FC}{CG}=\frac{CD}{GB}$．

Answer 1

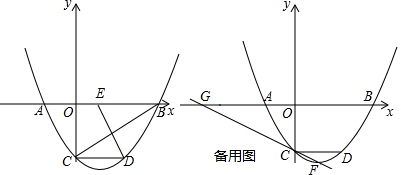
分析 （1）设出函数的表达式，代入C（0，-3），m=-1，求出即可；
（2）根据题意转化为证明四边形ECDB是菱形，根据菱形的定义判断即可得出E点坐标；
（3）求出抛物线顶点坐标，从而求出直线FC的方程，解出G点坐标，从而求出比值．

解答 解：（1）设函数为 y=a（x-m）（x+3m），（m＜0）
∵函数经过C（0，-3），代入解析式得：-3=-3am²
∵m=-1，
∴a=1，
∴该抛物线所表示的函数关系式为：y=（x+1）（x-3）=x²-2x-3；

（2）如图所示：
∵A（m，0），B（-3m，0），C（0，-3）
抛物线的解析式可设为：y=a（x-m）（x+3m），
把C（0，-3）代入得：a=$\frac{1}{{m}^{2}}$，
∴y=$\frac{1}{{m}^{2}}$（x-m）（x+3m），
令y=-3，
则-3=$\frac{1}{{m}^{2}}$（x-m）（x+3m），
解得：x₁=0，x₂=-2m，
故D（-2m，-3），
如果要求ED，CB垂直平分，则就是ECDB为菱形．
就是要在x轴上找到E，使得EC∥DB，且EC=CD=BD，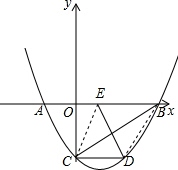
可求出CD=-2m，BD=$\sqrt{9+{m}^{2}}$，显然：m=-$\sqrt{3}$，CD=BD，
故以C，D，B，E为顶点的四边形是可能构成菱形的，
此时BE=CD=2$\sqrt{3}$，则OE=$\sqrt{3}$，故E点坐标为：（$\sqrt{3}$，0），所以可能存在点E满足题意；

（3）由（2）得抛物线的解析式为：y=$\frac{1}{{m}^{2}}$（x-m）（x+3m），
∴F（-m，-4），
又C（0，-3），
设CF直线解析式为：y=kx-3，
则-4=-mk-3，
解得：k=$\frac{1}{m}$，
所以CF直线解析式为：y=$\frac{1}{m}$x-3，
∴G（3m，0），
∴CF=$\sqrt{{m}^{2}+1}$，CG=3$\sqrt{{m}^{2}+1}$，CD=-2m，GB=-6m．
∴$\frac{FC}{GC}$=$\frac{CD}{GB}$=3．

点评 本题考查了求抛物线的解析式问题、菱形的判定、线段成比例问题以及二次函数综合应用，正确表示出CF，CG的长是解题关键．