
���� ��1����a��b��c��ֵ���룬������ߵ�ֵ�����ɵó��𰸣�
��2�����ݶ���ʽ���Զ���ʽ������������жϼ��ɣ�
��3�����ɱ߳�Ϊa+b+c�������Σ����ɵó��𰸣�
��� �⣺��1���ߵ�a=1��b=2��c=3ʱ����a+b+c��2=��1+2+3��2=36
a2+b2+c2=12+22+32=14��
�ࣨa+b+c��2��a2+b2+c2��
��2���ߣ�a+b+c��2=��a+b+c����a+b+c��
=a2+ab+ac+ab+b2+bc+ac+bc+c2
=a2+b2+c2+2ab+2bc+2ac��
�ࣨa+b+c��2��a2+b2+c2��
��3����ͼ��ʾ����a+b+c��2=a2+b2+c2+ab+ac+bc+ab+ac+bc��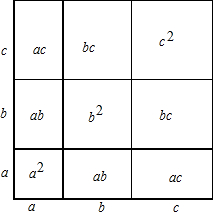
����a+b+c��2��a2+b2+c2��
���� ���⿼������ʽ�����㷨���Ӧ�ã�����ȷ������ʽ�����㷨����л����ǽ����Ĺؼ���Ҳ������ѧ���Ķ��ֲ���������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
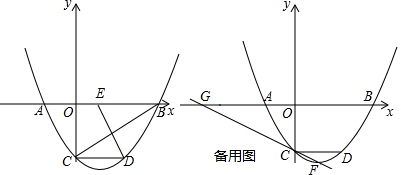
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
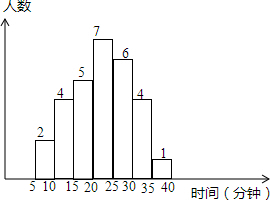 һ��ѧϰС���ij��˫�����ڼҲμӼ����Ͷ����õĴ���ʱ�䣨�������ƣ����˳������飬���ͼ����Ϣ�������С������ȡ������������29��
һ��ѧϰС���ij��˫�����ڼҲμӼ����Ͷ����õĴ���ʱ�䣨�������ƣ����˳������飬���ͼ����Ϣ�������С������ȡ������������29���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
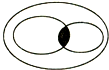 ��֪ʶ�ṹ������ƽ���ı��Ρ����Ρ����Ρ������εİ�����ϵ������ͼ��ʾ��������������Բ��ʾ����ƽ���ı��Σ���Ӱ���ֱ�ʾ���������Σ�
��֪ʶ�ṹ������ƽ���ı��Ρ����Ρ����Ρ������εİ�����ϵ������ͼ��ʾ��������������Բ��ʾ����ƽ���ı��Σ���Ӱ���ֱ�ʾ���������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com