
 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,∠BAC的平分线AD长为8cm,则BC=12cm.
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,∠BAC的平分线AD长为8cm,则BC=12cm. 分析 因为AD是∠BAC的平分线,∠BAC=60°,在Rt△ACD中,可利用勾股定理求得DC,进一步求得AC;求得∠ABC=30°,在Rt△ABC中,可求得AB,最后利用勾股定理求出BC.
解答 解:∵AD是∠BAC的平分线,∠BAC=60°,
∴∠DAC=30°,
∴DC=$\frac{1}{2}$AD=4cm,
∴AC=$\sqrt{A{D}^{2}-D{C}^{2}}$=4$\sqrt{3}$,
∵在△ABC中,∠C=90°,∠BAC=60°,
∴∠ABC=30°,
∴AB=2AC=8$\sqrt{3}$,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=12cm.
故答案为:12cm.
点评 本题考查了角平分线的定义,含30°直角三角形的性质,勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.


科目:初中数学 来源: 题型:解答题
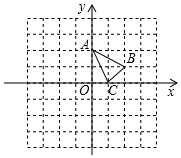 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1使它与△ABC的相似比为2,则点B的对应点B1的坐标是(4,2)或(-4,-2).
如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1使它与△ABC的相似比为2,则点B的对应点B1的坐标是(4,2)或(-4,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
| 发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
| 发芽种子频率$\frac{m}{n}$ | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是150米.
如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是150米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
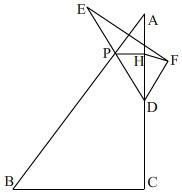 在△ABC中,∠ACB=Rt∠,BC=6,AC=8,点D是AC的中点,点P为AB边上的动点(P不与A重合),AP=t(t>0),PH⊥AC于点H,则PH=$\frac{3}{5}$t,连结DP并延长至点E,使得PE=PD,作点E关于AB的对称点F,连结FH.
在△ABC中,∠ACB=Rt∠,BC=6,AC=8,点D是AC的中点,点P为AB边上的动点(P不与A重合),AP=t(t>0),PH⊥AC于点H,则PH=$\frac{3}{5}$t,连结DP并延长至点E,使得PE=PD,作点E关于AB的对称点F,连结FH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com