
【题目】如图,∠AOB=165°,OD平分∠AOC.
(1)若∠AOD=50°,求∠BOC度数;
(2)若∠BOD=110°,那么OC是∠BOD的平分线吗?说明理由.
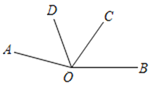
【答案】(1)65°;(2)OC是∠BOD的平分线,理由详见解析.
【解析】
(1)根据角平分线的定义可求得∠AOC的度数,然后根据角的和差即可求得结果;
(2)根据角平分线的定义和角的和差关系依次求出∠AOD和∠COD的度数,即得∠BOC和∠COD的关系,进而可作判断.
解:(1)∵OD平分∠AOC,∠AOD=50°,
∴∠AOC=2∠AOD=100°.
∴∠BOC=∠AOB-∠AOC=165°-100°=65°;
(2)OC是∠BOD的平分线,理由是:
∵∠AOB=165°,∠BOD=110°,
∴∠AOD=∠AOB-∠BOD=165°-110°=55°.
∵OD平分∠AOC,∴∠COD=∠AOD=55°.
∴∠BOC=∠BOD-∠COD=110°-55°=55°.
∴∠BOC=∠COD.
∴OC是∠BOD的平分线.


科目:初中数学 来源: 题型:
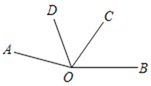
【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>x+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
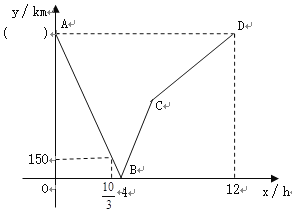
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图像回答以下问题:
(1)请在图中的( )内填上正确的值,并写出两车的速度和.
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
(3)请直接写出两车之间的距离不超过15km的时间范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.

(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为鼓励市民节约用水,特制定如下的收费标准:若每月每户用水不超过10立方米,则按3元/立方米的水价收费,并加收0.2元/立方米的污水处理费;若超过10立方米,则超过的部分按4元/立方米的水价收费,污水处理费不变.
(1)若小华家5月份的用水量为8立方米,那么小华家5月份的水费为_______元;
(2)若小华家6月份的用水量为15立方米,那么小华家6月份的水费为_______元;
(3)若小华家某个月的用水量为a(a>10)立方米,求小华家这个月的水费(用含a的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
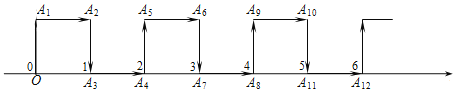
【题目】如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置O点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移动到![]() ,第2次移动到
,第2次移动到![]() ,第3次移动到
,第3次移动到![]() ,……,第n次移动到
,……,第n次移动到![]() ,则△O
,则△O![]() 的面积是( )
的面积是( )
A.504B.![]() C.
C.![]() D.505
D.505
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线![]() 平行于直线EC,且直线
平行于直线EC,且直线![]() 与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线
与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线![]() 上, 则DF的长为_____
上, 则DF的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点(A点在B点左侧),与
轴交于A、B两点(A点在B点左侧),与![]() 轴交于点C,连接BC、AC,tan∠OCB -tan∠OCA=1,OB=4OA.
轴交于点C,连接BC、AC,tan∠OCB -tan∠OCA=1,OB=4OA.
(1)求![]() 和b的值;
和b的值;
(2)点E在线段BC上,点F在BC的延长线上,且BE=CF,点D是直线BC下方抛物线上一点,当△EDF是以EF为斜线的直角三角形,且4ED=3FD时,求D点坐标;
(3)在(2)的条件下,过点A作AG⊥![]() 轴,R为抛物线上CD段上一点,连接AR,点K在AR上,连接DK并延长交AG于点G,连接DR,且2∠RDK+∠RKD=90°,∠GAR=∠RDK,若点M(
轴,R为抛物线上CD段上一点,连接AR,点K在AR上,连接DK并延长交AG于点G,连接DR,且2∠RDK+∠RKD=90°,∠GAR=∠RDK,若点M(![]() )w为坐标平面内一点,直线MD与直线BC交于点N,当MN=DN时,求△MRD的面积.
)w为坐标平面内一点,直线MD与直线BC交于点N,当MN=DN时,求△MRD的面积.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com