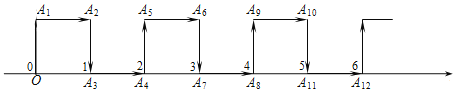
【题目】如图，在纸面所在的平面内，一只电子蚂蚁从数轴上表示原点的位置O点出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其移动路线如图所示，第1次移动到
，第2次移动到
，第3次移动到
，……，第n次移动到
，则△O
的面积是（ ）
A.504B.
C.
D.505
互动英语系列答案科目：初中数学 来源： 题型：
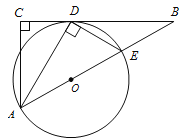
【题目】已知：如图，在△ABC 中，∠C=90°，∠BAC 的平分线 AD 交 BC于点 D，过点 D 作 DE⊥AD 交 AB 于点 E，以 AE 为直径作⊙O．
（1）求证：BC 是⊙O 的切线；
（2）若 AC=3，BC=4，求 BE 的长．
（3）在（2）的条件中，求 cos∠EAD 的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
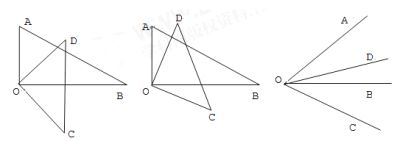
【题目】（1） 将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起， ∠AOB=∠DOC=90°.
①如图（1），若OD是∠AOB的平分线时，求∠BOD和∠AOC的度数.
②如图（2），若OD不是∠AOB的平分线，试猜想∠AOC与∠BOD的数量关系，并说明理由.
（2）如图（3），如果两个角∠AOB = ∠DOC= m°(0< m <90)，直接写出∠AOC与∠BOD的数量关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
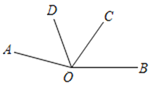
【题目】如图，∠AOB=165°，OD平分∠AOC．
（1）若∠AOD=50°，求∠BOC度数；
（2）若∠BOD=110°，那么OC是∠BOD的平分线吗？说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
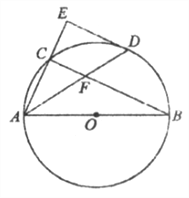
【题目】如图，△ABC内接于⊙O，AB为直径，点D在⊙O上，过点D作⊙O切线与AC的延长线交于点E，ED∥BC，连接AD交BC于点F.
（1）求证：∠BAD＝∠DAE；
（2）若AB＝6，AD＝5，求DF的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,直线y=x+m与y=nx+4n(n≠0)的交点的横坐标为2,则关于x的不等式x+m>nx+4n>0的整数解为 ( )
A. 1B. 3C. 4D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，两个形状、大小完全相同的含有
、
的直角三角板如图①放置，
、
与直线
重合，且三角板
、三角板
均可绕点
逆时针旋转.
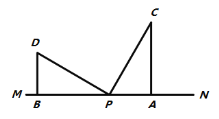
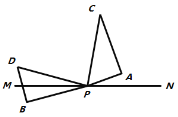
图① 图②
（1）直接写出
的度数是______.
（2）如图②，在图①基础上，若三角板的边从
处开始绕点逆时针旋转，转速为4.5度/秒，同时三角板的边从
处开始绕点逆时针旋转，转速为0.5度/秒，（当转到与重合时，两三角板都停止转动），在旋转过程中，当
与重合时，求旋转的时间是多少？
（3）在（2）的条件下，、、
三条射线中，当其中一条射线平分另两条射线的夹角时，请求出旋转的时间.
查看答案和解析>>
科目：初中数学 来源： 题型：
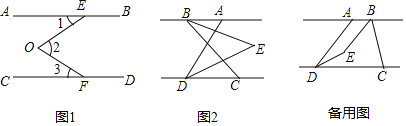
【题目】已知AB∥CD．
（1）如图1，EOF是直线AB、CD间的一条折线，猜想∠1、∠2、∠3的数量关系，并说明理由；
（2）如图2，若点C在点D的右侧，BE平分∠ABC，DE平分∠ADC，BE、DF所在直线交于点E，若∠ADC＝α，∠ABC＝β，求∠BED的度数（用含有α、β的式子表示）；
（3）在（2）的前提下将线段BC沿DC方向平移，使得点B在点A的右侧，其他条件不变，若∠ADC＝α，∠ABC＝β，求∠BED的度数（用含有α、β的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，过平行四边形ABCD对角线交点O的线段EF，分别交AD，BC于点E，F，当AE＝ED时，△AOE的面积为4，则四边形EFCD的面积是（ ）
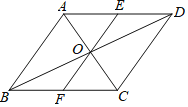
A.8B.12C.16D.32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
