
【题目】已知AB∥CD.
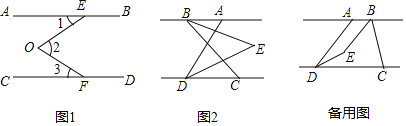
(1)如图1,EOF是直线AB、CD间的一条折线,猜想∠1、∠2、∠3的数量关系,并说明理由;
(2)如图2,若点C在点D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DF所在直线交于点E,若∠ADC=α,∠ABC=β,求∠BED的度数(用含有α、β的式子表示);
(3)在(2)的前提下将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ADC=α,∠ABC=β,求∠BED的度数(用含有α、β的式子表示).
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)过O作OM∥AB,利用平行线的性质和等量代换,可得∠2=∠1+∠3;
(2)过E作EN∥AB,则EN∥AB∥CD,利用平行线的性质,角平分线的性质可以得到![]() ;
;
(3)过E作EP∥AB,则EP∥AB∥CD,利用平行线的性质,两直线平行,内错角相等,同旁内角互补,再利用等量代换得出结论.
(1)如图1,
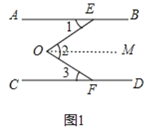
过O作OM∥AB,
∵AB∥CD,
∴AB∥CD∥0M,
∴∠1=∠EOM,∠3=∠FOM,
∵∠EOF=∠EOM+∠FOM,
∴∠2=∠1+∠3;
(2)如图2,
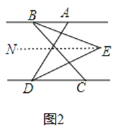
过E作EN∥AB,则EN∥AB∥CD,
∴∠BEN=∠ABE,∠DEN=∠CDE
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠EBC=![]() ∠ABC,∠ADE=∠CDE=
∠ABC,∠ADE=∠CDE=![]() ∠ADC,
∠ADC,
∴∠BED=∠ABE+∠CDE=![]() α+
α+![]() β;
β;
(3)如图3,
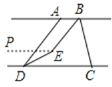
图3
过E作EP∥AB,则EP∥AB∥CD,
∴∠PED=∠EDC,∠PEB+∠ABE=180°,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠EBC=![]() ∠ABC,∠ADE=∠CDE=
∠ABC,∠ADE=∠CDE=![]() ∠ADC,
∠ADC,
∴∠BED=∠PED+∠PEB=![]() α+(180°﹣
α+(180°﹣![]() β)=
β)=![]() α﹣
α﹣![]() β+180°
β+180°


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
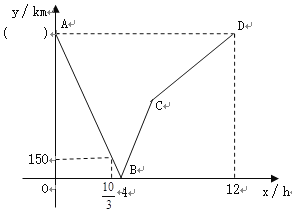
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图像回答以下问题:
(1)请在图中的( )内填上正确的值,并写出两车的速度和.
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
(3)请直接写出两车之间的距离不超过15km的时间范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
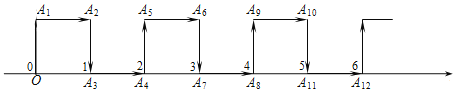
【题目】如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置O点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移动到![]() ,第2次移动到
,第2次移动到![]() ,第3次移动到
,第3次移动到![]() ,……,第n次移动到
,……,第n次移动到![]() ,则△O
,则△O![]() 的面积是( )
的面积是( )
A.504B.![]() C.
C.![]() D.505
D.505
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线![]() 平行于直线EC,且直线
平行于直线EC,且直线![]() 与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线
与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线![]() 上, 则DF的长为_____
上, 则DF的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的长为6,宽为4,将长方形先向上平移2个单位,再向右平移2个单位得到长方形![]() ,则阴影部分面积是( )
,则阴影部分面积是( )
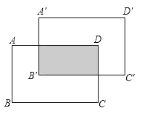
A.12B.10C.8D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,甲在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是( )米

A. 150 B. 175 C. 180 D. 225
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点(A点在B点左侧),与
轴交于A、B两点(A点在B点左侧),与![]() 轴交于点C,连接BC、AC,tan∠OCB -tan∠OCA=1,OB=4OA.
轴交于点C,连接BC、AC,tan∠OCB -tan∠OCA=1,OB=4OA.
(1)求![]() 和b的值;
和b的值;
(2)点E在线段BC上,点F在BC的延长线上,且BE=CF,点D是直线BC下方抛物线上一点,当△EDF是以EF为斜线的直角三角形,且4ED=3FD时,求D点坐标;
(3)在(2)的条件下,过点A作AG⊥![]() 轴,R为抛物线上CD段上一点,连接AR,点K在AR上,连接DK并延长交AG于点G,连接DR,且2∠RDK+∠RKD=90°,∠GAR=∠RDK,若点M(
轴,R为抛物线上CD段上一点,连接AR,点K在AR上,连接DK并延长交AG于点G,连接DR,且2∠RDK+∠RKD=90°,∠GAR=∠RDK,若点M(![]() )w为坐标平面内一点,直线MD与直线BC交于点N,当MN=DN时,求△MRD的面积.
)w为坐标平面内一点,直线MD与直线BC交于点N,当MN=DN时,求△MRD的面积.



查看答案和解析>>
科目:初中数学 来源: 题型:
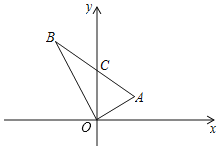
【题目】如图,在平面直角坐标系中,O为原点,点A(2,1),B(﹣2,4),直线AB与y轴交于点C.
(1)求点C的坐标;
(2)求证:△OAB是直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com