计算:${^{-1}}-\root{3}{8}-{({\sqrt{2}sin45°-2007})^0}$．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

3．计算：${（{\frac{1}{2}}）^{-1}}-\root{3}{8}-{（{\sqrt{2}sin45°-2007}）^0}$．

分析原式第一项利用负指数幂法则计算，第二项利用立方根定义计算，最后一项利用零指数幂法则计算即可得到结果．

解答解：原式=2-2-1=-1．

点评此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

练习册系列答案

千里马走向假期期末仿真试卷寒假系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

4．计算8²⁰¹³×（-0.125）²⁰¹⁴=0.125．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

5．在实数3.14，$\frac{1}{4}$，$\sqrt{2}$，0.$\stackrel{•}{3}$，0.00182732…，3π，π，-$\sqrt{3}$，$\sqrt{4}$中，有理数有3.14，$\frac{1}{4}$，0.$\stackrel{•}{3}$，$\sqrt{4}$，无理数有$\sqrt{2}$，0.00182732…，3π，π，-$\sqrt{3}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．计算：
（1）$3\frac{1}{4}+（-2\frac{3}{5}）+5\frac{3}{4}+（-8\frac{2}{5}）$；
（2）12-（-18）+（-7）-15；
（3）$（-2\frac{1}{5}）+（-3\frac{4}{5}）-（-4\frac{1}{2}）$；
（4）$（\frac{2}{3}）+\frac{1}{2}+\frac{4}{5}+（-\frac{1}{2}）+（-\frac{1}{3}）$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．计算：
（1）$\sqrt{50}$×$\sqrt{8}$-21；
（2）（3+$\sqrt{5}$）（$\sqrt{5}$-2）；
（3）$\sqrt{40}$-5$\sqrt{\frac{1}{10}}$+$\sqrt{10}$；
（4）（$\sqrt{24}$-$\sqrt{\frac{1}{6}}$）÷$\sqrt{3}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

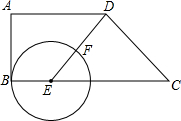在梯形ABCD中，AD∥BC，AB⊥AD，AB=4，AD=5，CD=5．E为底边BC上一点，以点E为圆心，BE为半径画⊙E交射线ED于点F．设BE=y，DF=x．
（1）求BC的长度及sin∠C的值；
（2）如图，当点F在线段DE上时，
①试求y关于x的函数关系式
②当以CD直径的⊙O与⊙E与相切时，求y的值；
（3）连接AF、BF，当△ABF是以AF为腰的等腰三角形时，直接写出所有y的值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．

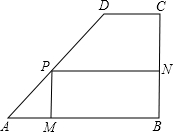学校校园内有一块形状为直角梯形的空地ABCD，其中AB∥DC，∠B=90°，AB=100m，BC=80m，CD=40m，现计划在上面建设一个面积为S的矩形综合楼PMBN，其中点P在线段AD上，且PM的长至少为36m
（1）求边AD的长；
（2）设PA=xm，求S关于X的函数关系式，并指出自变量x的取值范围；
（3）若S=2800m²，求PA的长；
（4）当x的值为多少时，s的值最大，最大值为多少？
（5）求tan$\frac{A}{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

12．已知∠AOB=65°，∠BOC=15°，则∠AOC等于（　　）

A．

80°

B．

40°

C．

80°或40°

D．

以上都不对

查看答案和解析>>