
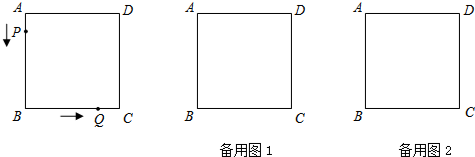
 дкЬнаЮABCDжаЃЌADЁЮBCЃЌABЁЭADЃЌAB=4ЃЌAD=5ЃЌCD=5ЃЎEЮЊЕзБпBCЩЯвЛЕуЃЌвдЕуEЮЊдВаФЃЌBEЮЊАыОЖЛЁбEНЛЩфЯпEDгкЕуFЃЎЩшBE=yЃЌDF=xЃЎ
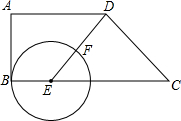
дкЬнаЮABCDжаЃЌADЁЮBCЃЌABЁЭADЃЌAB=4ЃЌAD=5ЃЌCD=5ЃЎEЮЊЕзБпBCЩЯвЛЕуЃЌвдЕуEЮЊдВаФЃЌBEЮЊАыОЖЛЁбEНЛЩфЯпEDгкЕуFЃЎЩшBE=yЃЌDF=xЃЎЗжЮі ЃЈ1ЃЉШчЭМ1ЃЌзїИЈжњЯпЃЛдЫгУОиаЮЕФаджЪЃЌНсКЯЙДЙЩЖЈРэЃЌМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉЂйдЫгУЙДЙЩЖЈРэСаГіЙигкxЁЂyЕФЙиЯЕЪНЃЈx+yЃЉ2=42+ЃЈ5-yЃЉ2ЃЌЧѓГіyМДПЩНтОіЮЪЬтЃЎ
ЂкШчЭМЂйЃЌзїИЈжњЯпЃЛдЫгУЗжРрЬжТлЕФЪ§бЇЫМЯыЃЌАДЁбOгыЁбEФкЧаЛђЭтЧаСНжжЧщПіРДЗжРрНтЮіЃЛНшжњЙДЙЩЖЈРэСаГіЙигкyЕФЗНГЬЃЌЧѓГіyЃЌМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉШчЭМ2ЛђЭМ3ЃЌдЫгУЗжРрЬжТлЕФЪ§бЇЫМЯыЃЌАДЕБFA=FBЛђFA=ABЪБЃЌСНжжЧщПіРДЗжРрНтЮіЃЛНшжњШ§НЧаЮЕФУцЛ§ЙЋЪНЛђЙДЙЩЖЈРэСаГіЙигкyЕФЗНГЬЃЌЧѓГіyМДПЩНтОіЮЪЬтЃЎ
НтД№ НтЃКЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуDзїDGЁЭBCгкЕуGЃЛ
ЁпADЁЮBCЃЌABЁЭADЃЌ
ЁрЫФБпаЮABGDЮЊОиаЮЃЌ
ЁрDG=AB=4ЃЌBG=AD=5ЃЛгЩЙДЙЩЖЈРэЕУЃК
CG=$\sqrt{C{D}^{2}-D{G}^{2}}$=3ЃЌ
ЁрBC=8ЃЌsinЁЯC=$\frac{DG}{DC}=\frac{4}{5}$ЃЎ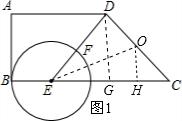 ЃЈ2ЃЉЂйЃЌШчЭМ1ЃЌEG=5-yЃЛ
ЃЈ2ЃЉЂйЃЌШчЭМ1ЃЌEG=5-yЃЛ
гЩЙДЙЩЖЈРэЕУЃКDE2=DG2+EG2ЃЌМДЃЈx+yЃЉ2=42+ЃЈ5-yЃЉ2ЃЌ
Ёрy=$\frac{41-{x}^{2}}{2x+10}$ЃЎ
ЂкШчЭМ1ЃЌЩшCDЕФжаЕуЮЊOЃЌСЌНгEOЃЛ
Й§ЕуOзїOHЁЭBCгкЕуHЃЛдђOHЁЮDGЃЌOC=$\frac{5}{2}$ЃЛ
ЁрGH=CH=ЃЌOH=DG=2ЃЌEH=8-y-
ЕБЁбOгыЁбEЭтЧаЪБЃЌOE=y+$\frac{5}{2}$ЃЛдкжБНЧЁїOEHжаЃЌ
OE2=OH2+EH2ЃЌМД$ЃЈy+\frac{5}{2}ЃЉ^{2}=ЃЈ\frac{13}{2}-yЃЉ^{2}+{2}^{2}$
НтЕУЃКy=$\frac{20}{9}$ЃЛ
ЕБЁбOгыЁбEФкЧаЪБЃЌOE=|y-$\frac{5}{2}$|ЃЛдкжБНЧЁїOEHжаЃЌ
OE2=OH2+EH2ЃЌМД$ЃЈy-\frac{5}{2}ЃЉ^{2}=ЃЈ\frac{13}{2}-yЃЉ^{2}+{2}^{2}$ЃЌ
НтЕУЃКy=5ЃЎ
злЩЯЫљЪіЃЌЕБЁбOгыЁбEЯрЧаЪБЃЌy=$\frac{20}{9}$Лђ5ЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгAFЁЂAEЃЛЕБAF=AB=4ЪБЃЌ
дкЁїABEгыЁїAFEжаЃЌ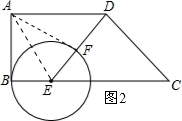
$\left\{\begin{array}{l}{AB=AF}\\{AE=AE}\\{BE=FE}\end{array}\right.$ЃЌ
ЁрЁїABEЁеЁїAFEЃЈSSSЃЉЃЌ
ЁрЁЯAFE=ЁЯABE=90ЁуЃЌAF=AB=4ЃЛ
гЩЙДЙЩЖЈРэЕУЃКDF=$\sqrt{{5}^{2}-{4}^{2}}$=3ЃЛ
гЩШ§НЧаЮЕФУцЛ§ЙЋЪНЕУЃК
$\frac{1}{2}AD•AB=\frac{1}{2}DE•AF$ЃЌ
НтЕУЃКDE=5ЃЌ
ЁрBE=EF=5-3=2ЃЌМДy=2ЃЎ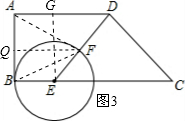 ШчЭМ3ЃЌЕБFA=FBЪБЃЌ
ШчЭМ3ЃЌЕБFA=FBЪБЃЌ
Й§ЕуFзїQFЁЭABгкЕуQЃЌЙ§ЕуEзїEGЁЭDAгкЕуGЃЛ
дђAQ=BQЃЌEG=BA=4ЃЌAG=BE=yЃЛ
ЁпADЁЮBCЁЮFQЃЌ
ЁрDF=EF=yЃЛ
гЩЙДЙЩЖЈРэЕУЃКЃЈ2yЃЉ2=42+ЃЈ5-yЃЉ2ЃЌ
НтЕУЃКy=$\frac{2\sqrt{37}-5}{3}$ЃЌ
злЩЯЫљЪіЃЌЕБЁїABFЪЧвдAFЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌyЕФЫљгаШЁжЕЮЊ2Лђ$\frac{2\sqrt{37}-5}{2}$ЃЎ
ЕуЦР ИУЬтвджБНЧЬнаЮКЭдВЮЊдиЬхЃЌвдПМВщЙДЙЩЖЈРэЁЂЯрЧаСНдВЕФаджЪЁЂЕШбќШ§НЧаЮЕФаджЪМАЦфгІгУЕШМИКЮжЊЪЖЕуЮЊКЫаФЙЙдьЖјГЩЃЛНтЬтЕФЗНЗЈЪЧзїИЈжњЯпЃЌНЋЗжЩЂЕФЬѕМўМЏжаЃЛНтЬтЕФЙиМќЪЧСщЛюдЫгУЙДЙЩЖЈРэЁЂЯрЧаСНдВЕФаджЪЕШжЊЪЖЕуРДЗжЮіЁЂХаЖЯЁЂЭЦРэЛђНтД№ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
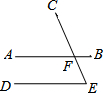 ШчЭМЃЌABЁЮDEЃЌЁЯE=65ЁуЃЌдђЁЯAFCЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ
ШчЭМЃЌABЁЮDEЃЌЁЯE=65ЁуЃЌдђЁЯAFCЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 135Ёу | BЃЎ | 115Ёу | CЃЎ | 36Ёу | DЃЎ | 65Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
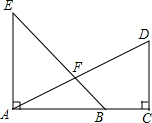 ШчЭМЃЌвбжЊAEЁЭACЃЌDCЁЭACЃЌAE=ACЃЌAB=CDЃЌADгыBEЛЅЯрДЙжБЧвЯрЕШТ№ЃПЮЊЪВУДЃП
ШчЭМЃЌвбжЊAEЁЭACЃЌDCЁЭACЃЌAE=ACЃЌAB=CDЃЌADгыBEЛЅЯрДЙжБЧвЯрЕШТ№ЃПЮЊЪВУДЃПВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
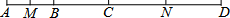 ШчЭМЃЌABЃКBCЃКCD=2ЃК3ЃК4ЃЌMЪЧABЕФжаЕуЃЌNЪЧCDЕФжаЕуЃЌ
ШчЭМЃЌABЃКBCЃКCD=2ЃК3ЃК4ЃЌMЪЧABЕФжаЕуЃЌNЪЧCDЕФжаЕуЃЌВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
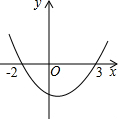 ШчЭМЪЧХзЮяЯпy=ax2+bx+cЕФЭМЯѓЃЌдђвЛдЊЖўДЮЗНГЬax2+bx+c=0ЕФНтЪЧx1=-2ЃЌx2=3ЃЎ
ШчЭМЪЧХзЮяЯпy=ax2+bx+cЕФЭМЯѓЃЌдђвЛдЊЖўДЮЗНГЬax2+bx+c=0ЕФНтЪЧx1=-2ЃЌx2=3ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
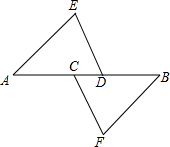 ШчЭМЃКЕуCЁЂDдкABЩЯЃЌЧвAC=BDЃЌAE=FBЃЌDE=FCЃЎЧѓжЄЃКAEЁЮBFЃЎ
ШчЭМЃКЕуCЁЂDдкABЩЯЃЌЧвAC=BDЃЌAE=FBЃЌDE=FCЃЎЧѓжЄЃКAEЁЮBFЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com