
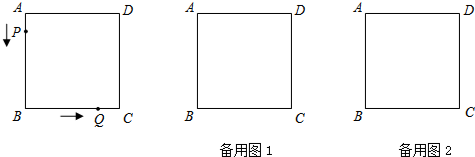
���� ��1�������ı���ABCD�DZ߳�Ϊ6�������Σ����������ABCD���ܳ�Ϊ24��Ȼ������߶�PQ��������ABCD���ܳ���Ϊ1��2�������֣��������ֵ��ܳ��ֱ�Ϊ��8��16��Ȼ��֢ٵ�Q����BC��ʱ����0��t��2ʱ���ڵ�Q����CD��ʱ����2��t��4ʱ���۵�Q����AD��ʱ����4��t��6ʱ3��������ۼ��ɣ�
��2�������������ABCD�����Ϊ36��Ȼ������߶�PQ��������ABCD�������Ϊ1��3�����֣��������ֵ�����ֱ�Ϊ��9��27��Ȼ��֢ٵ�Q����BC��ʱ����0��t��2ʱ���ڵ�Q����CD��ʱ����2��t��4ʱ���۵�Q����AD��ʱ����4��t��6ʱ3��������ۼ��ɣ�
��� �⣺��1������ʱ��t��ʹ�߶�PQ��������ABCD���ܳ���Ϊ1��2�������֣�
���ı���ABCD�DZ߳�Ϊ6�������Σ�
��������ABCD���ܳ�Ϊ24��
��PQ��������ABCD���ܳ���Ϊ1��2�������֣�
�������ֵ��ܳ��ֱ�Ϊ��24��$\frac{1}{3}$=8��24��$\frac{2}{3}$=16��
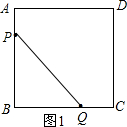
�ٵ�Q����BC��ʱ����0��t��2ʱ����ͼ1��ʾ��
�߶���P���˶��ٶ�Ϊÿ��1����λ������Q���˶��ٶ�Ϊÿ��3����λ��
�ྭ��t�룬AP=t��BQ=3t��
��BP=6-t��QC=6-3t����BP+BQ=6+2t��AP+AD+DC+QC=24-6-2t��
��BP+BQ=$\frac{1}{2}$��AP+AD+DC+QC����
��6+2t=$\frac{1}{2}$��24-6-2t����
��ã�t=1��
�ڵ�Q����CD��ʱ����2��t��4ʱ����ͼ2��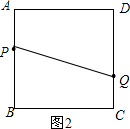
�߶���P���˶��ٶ�Ϊÿ��1����λ������Q���˶��ٶ�Ϊÿ��3����λ��
�ྭ��t�룬AP=t��QC=3t-6��
��BP=6-t��DQ=12-3t��
��BP+BC+QC=6-t+6+3t-6=6+2t��AP+AD+DQ=18-2t��
��BP+BC+QC=$\frac{1}{2}$��AP+AD+DQ������BP+BC+QC=2��AP+AD+DQ����
��6+2t=$\frac{1}{2}$��18-2t������6+2t=2��18-2t����
��ã�t=1��t=7��������������ȥ��
�۵�Q����AD��ʱ����4��t��6ʱ����ͼ3��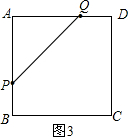
�߶���P���˶��ٶ�Ϊÿ��1����λ������Q���˶��ٶ�Ϊÿ��3����λ��
�ྭ��t�룬AP=t��QD=3t-12��
��BP=6-t��AQ=18-3t��
��AP+AQ=18-2t��BP+BC+CD+DQ=24-��18-2t��=6+2t��
��AP+AQ=$\frac{1}{2}$��BP+BC+CD+DQ����
��18-2t=12��6+2t����
��ã�t=5��
�൱tȡ1���5�룬ʹ�߶�PQ��������ABCD���ܳ���Ϊ1��2�������֣�
��2������ʱ��t��ʹ�߶�OQ��������ABCD�������Ϊ1��3�����֣�
���ı���ABCD�DZ߳�Ϊ6�������Σ�
��������ABCD�����Ϊ36��
��PQ��������ABCD�������Ϊ1��3�������֣�
�������ֵ�����ֱ�Ϊ��36��$\frac{1}{4}$=9��36��$\frac{3}{4}$=27��
�ٵ�Q����BC��ʱ����0��t��2ʱ����ͼ1��ʾ��
�ɣ�1���еĢ�֪��BP=6-t��BQ=3t��
��S��BPQ=$\frac{1}{2}$BP•BQ��
��S��BPQ=$\frac{1}{2}$��6-t��•3t��
��$\frac{1}{2}$��6-t��•3t=9ʱ��
��ã�t1=3+$\sqrt{3}$����ȥ����t2=3-$\sqrt{3}$��
��$\frac{1}{2}$��6-t��•3t=27ʱ��
��ã��⣻
�ڵ�Q����CD��ʱ����2��t2��4ʱ����ͼ2��ʾ��
�ɣ�1���еĢ�֪��BP=6-t��QC=3t-6��
��S����PBCQ=$\frac{1}{2}$��QC+BP��•BC��
��S����PBCQ=$\frac{1}{2}$��3t-6+6-t����6��
��$\frac{1}{2}$��3t-6+6-t����6=9ʱ��
��ã�t=1.5����ȥ����
��$\frac{1}{2}$��3t-6+6-t����6=27ʱ��
��ã�t=4.5����ȥ����
�۵�Q����AD��ʱ����4��t��6ʱ����ͼ3��
�ɣ�1���еĢ�֪��AP=t��AQ=18-3t��
��S��APQ=$\frac{1}{2}$AP•AQ��
��S��APQ=$\frac{1}{2}$•t•��18-3t����
��$\frac{1}{2}$t��18-3t��=9ʱ��
��ã�t1=3+$\sqrt{3}$��t2=3-$\sqrt{3}$����ȥ����
��$\frac{1}{2}$t��18-3t��=27ʱ��
��ã��⣮
�����ʱ��tΪ��3+$\sqrt{3}$�����3-$\sqrt{3}$���룬ʹ�߶�PQ��������ABCD�������Ϊ1��3�����֣�
���� ���⿼���������ε����ʡ��������ε��ܳ���������ر�����Ŀ���漰�Ķ������⣬��ѧ����˵��һ���ѵ㣬����Ĺؼ��ǣ��������ۢٵ�Q����BC��ʱ����0��t��2ʱ���ڵ�Q����CD��ʱ����2��t��4ʱ���۵�Q����AD��ʱ����4��t��6ʱ3��������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{9}$������ƽ������$\sqrt{3}$ | B�� | ��$\frac{3}{4}$��$\frac{9}{16}$������ƽ���� | ||
| C�� | -8����������2 | D�� | 0û��ƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
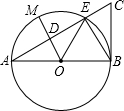 ��ͼ�����߶�ABΪֱ���ġ�O���߶�AC�ڵ�E����M��$\widehat{AE}$���е㣬OM��AC�ڵ�D����BOE=60�㣬cosC=$\frac{1}{2}$��BC=2$\sqrt{3}$����MD�ij���Ϊ��������
��ͼ�����߶�ABΪֱ���ġ�O���߶�AC�ڵ�E����M��$\widehat{AE}$���е㣬OM��AC�ڵ�D����BOE=60�㣬cosC=$\frac{1}{2}$��BC=2$\sqrt{3}$����MD�ij���Ϊ��������| A�� | $\frac{1}{2}$ | B�� | $\frac{3}{2}$ | C�� | 2 | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
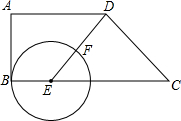 ������ABCD�У�AD��BC��AB��AD��AB=4��AD=5��CD=5��EΪ�ױ�BC��һ�㣬�Ե�EΪԲ�ģ�BEΪ�뾶����E������ED�ڵ�F����BE=y��DF=x��
������ABCD�У�AD��BC��AB��AD��AB=4��AD=5��CD=5��EΪ�ױ�BC��һ�㣬�Ե�EΪԲ�ģ�BEΪ�뾶����E������ED�ڵ�F����BE=y��DF=x���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
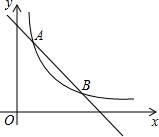 ��ͼ����ֱ������ϵ�У�ֱ��y=6-x�뺯��y=$\frac{5}{x}$��x��0����ͼ����A��B����A��x1��y1������ô��Ϊx1����Ϊy1�ľ��ε�������ܳ��ֱ���5��12��
��ͼ����ֱ������ϵ�У�ֱ��y=6-x�뺯��y=$\frac{5}{x}$��x��0����ͼ����A��B����A��x1��y1������ô��Ϊx1����Ϊy1�ľ��ε�������ܳ��ֱ���5��12���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com