
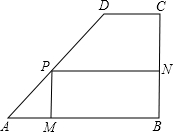
 学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m
学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m 分析 (1)可通过构建直角三角形进行求解,过D作AB的垂线,那么可在构建的直角三角形中,根据梯形两底的差和梯形的高,用勾股定理求出AD的长.
(2)可根据(1)中构建的直角三角形求出∠A的正弦和余弦值,然后在直角三角形AMP中,表示出AM,PM的长,进而可根据AB的长,表示出矩形的长BM的值,由此可根据矩形的面积公式得出关于S、x的函数关系式.自变量的取值范围可根据PM的长至少为36m来解,即让PM的表达式大于等于36即可.
(3)可将S的值代入(2)所求得的函数解析式中,求出x的值,然后看x的值是否符合自变量的取值范围.
(4)由S=$-\frac{12}{25}{x}^{2}$+80x=-$\frac{12}{25}(x-\frac{250}{3})^{2}+\frac{1000}{3}$,当x-$\frac{250}{3}$=0时,S有最大值,即可解答.
(5)在Rt△AED中,求得tanA=$\frac{DE}{AE}=\frac{80}{60}=\frac{4}{3}$,根据$tanA=\frac{2tan\frac{A}{2}}{1-ta{n}^{2}\frac{A}{2}}=\frac{4}{3}$,解得:$tan{\frac{A}{2}}_{1}=-2$,$tan{\frac{A}{2}}_{2}=\frac{1}{2}$,因为∠A为锐角,$tan\frac{A}{2}=\frac{1}{2}$.
解答 解:(1)过点D作DE⊥AB于E,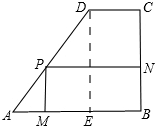
则DE∥BC且DE=BC,CD=BE,DE∥PM,
Rt△ADE中,DE=80m,
∴AE=AB-BE=100-40=60m,
∴AD=$\sqrt{A{E}^{2}+D{E}^{2}}=\sqrt{6{0}^{2}+8{0}^{2}}=100$m.
(2)∵DE∥PM
∴△APM∽△ADE
∴$\frac{AP}{AD}=\frac{PM}{DE}=\frac{AM}{AE}$,
即$\frac{x}{100}=\frac{PM}{80}=\frac{AM}{60}$,
∴PM=$\frac{4}{5}$x,AM=$\frac{3}{5}$x,
即MB=AB-AM=100-$\frac{3}{5}$x,
S=PM•MB=$\frac{4}{5}$x•(100-$\frac{3}{5}$x)=-$\frac{12}{25}{x}^{2}$+80x,
由PM=$\frac{4}{5}$x≥36,得x≥45
∴自变量x的取值范围为45≤x≤100.
(3)当S=2800m2时,
-$\frac{12}{25}{x}^{2}$+80x=2800,
12x2-2000x+70000=0,
3x2-500x+17500=0,
解得:${x}_{1}=\frac{350}{3}$,x2=50,
∵45≤x≤100,
∴x=50,
即PA=50m.
(4)S=$-\frac{12}{25}{x}^{2}$+80x=-$\frac{12}{25}(x-\frac{250}{3})^{2}+\frac{1000}{3}$,
当x-$\frac{250}{3}$=0时,S有最大值,
即x=$\frac{250}{3}$时,S有最大值,最大值为$\frac{1000}{3}$.
(5)在Rt△AED中,DE=80,AE=60,
∴tanA=$\frac{DE}{AE}=\frac{80}{60}=\frac{4}{3}$,
∵$tanA=\frac{2tan\frac{A}{2}}{1-ta{n}^{2}\frac{A}{2}}=\frac{4}{3}$,
解得:$tan{\frac{A}{2}}_{1}=-2$,$tan{\frac{A}{2}}_{2}=\frac{1}{2}$,
∵∠A为锐角,
∴$tan\frac{A}{2}=\frac{1}{2}$.
点评 本题结合实际问题考查了勾股定理、相似三角形的判定和性质、二次函数的应用、三角函数求值,解决本题的关键是正确的用x表示出矩形的长和宽,然后利用勾股定理,相似三角形以及二次函数的相关知识进行解答.


科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.当t=$\frac{5}{2}$或3或3.6时,△CBD是等腰三角形.
如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.当t=$\frac{5}{2}$或3或3.6时,△CBD是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
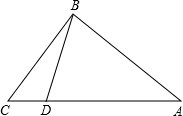
 如图,在Rt△ABC中,∠ABC=90°,在边AB上取一点D,使得DB=BC,过点D作EF⊥AC,分别交AC于点E,交CB的延长线于点F,求证:FC=AB+DB.
如图,在Rt△ABC中,∠ABC=90°,在边AB上取一点D,使得DB=BC,过点D作EF⊥AC,分别交AC于点E,交CB的延长线于点F,求证:FC=AB+DB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
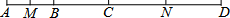 如图,AB:BC:CD=2:3:4,M是AB的中点,N是CD的中点,
如图,AB:BC:CD=2:3:4,M是AB的中点,N是CD的中点,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,线段AB表示一条对折的绳子,现从P点处将绳子剪断,剪断后的各段绳子中最长的一段为30cm,若AP=$\frac{2}{3}$BP,则原来绳长50或75cm.
如图,线段AB表示一条对折的绳子,现从P点处将绳子剪断,剪断后的各段绳子中最长的一段为30cm,若AP=$\frac{2}{3}$BP,则原来绳长50或75cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50°,80° | B. | 65°,65° | ||
| C. | 50°,80°或65°,65° | D. | 60°,70°或30°,100° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com