
 如图,线段AB表示一条对折的绳子,现从P点处将绳子剪断,剪断后的各段绳子中最长的一段为30cm,若AP=$\frac{2}{3}$BP,则原来绳长50或75cm.
如图,线段AB表示一条对折的绳子,现从P点处将绳子剪断,剪断后的各段绳子中最长的一段为30cm,若AP=$\frac{2}{3}$BP,则原来绳长50或75cm. 分析 分类讨论:①AP是最长的一段,根据AP=$\frac{2}{3}$BP,可得PB的长,再根据线段的和差,可得答案;②PB是最长的一段,根据AP=$\frac{2}{3}$BP,可得AP的长再根据线段的和差,可得答案.
解答 解:①AP是最长的一段,AP=30=$\frac{2}{3}$PB,得
PB=30×$\frac{3}{2}$=45,
由线段的和差,得
AB=AP+PB=30+45=75cm,
②PB是最长的一段,AP=$\frac{2}{3}$×30=20cm,
由线段的和差,得
AB=AP+PB=20+30=50cm,
故答案为:50或75.
点评 本题考查了两点间的距离,分类讨论是解题关键,以防遗漏.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
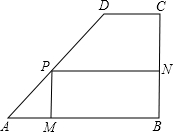 学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m
学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com