
【题目】在平面直角坐标系xOy中,点A的坐标为(0,m),且m≠0,点B的坐标为(n,0),将线段AB绕点B顺时针旋转90°.得到线段BA1,称点A1为点A关于点B的“伴随点”,图1为点A关于点B的“伴随点”的示意图
(1)已知点A(0,4),
①当点B的坐标分别为(1,0),(﹣2,0)时,点A关于点B的“伴随点”的坐标分别为 , ;
②点(x,y)是点A关于点B的“伴随点”,直接写出y与x之间的关系式;
(2)如图2,点C的坐标为(﹣3,0),以C为圆心,![]() 为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.

【答案】(1)①(5,1),(2,﹣2);②P1(x,y)是点A关于点B的“伴随点”,y与x之间的关系式为y=x﹣4;(2)m≤﹣1或m≥1.
【解析】
(1)①构造全等三角形求出点A1坐标即可;②取N(4,0),则OA=ON,作A1M⊥x轴于M,在△ABO≌△BA1M的条件下可得出△A1MN是等腰直角三角形,所以点A1在经过点N,与x轴的夹角为45°的直线上时,P1(x,y)是点A关于点B的“伴随点”,易得关系式为y=x﹣4;
(2)结合②中关系式,可得当直线y=x﹣m与⊙C有交点时,在⊙C上存在点A关于点B的“伴随点”,可求出 m的范围.
解:(1)①如图1中,作A1M⊥x轴于M.

∵AB=BA1,∠AOB=∠A1MB=90°,易证∠ABO=∠A1,
∴△ABO≌△BA1M(AAS)
∴OA=BM,OB=A1M,
当A(0,4),B(1,0)时,BM=4,A1M=1,OM=5,
∴A1(5,1),
当A(0,4),B(﹣2,0)时,同法可得A1(2,﹣2).
故答案为(5,1),(2,﹣2).
②如图2中,取N(4,0),则OA=ON,作A1M⊥x轴于M.
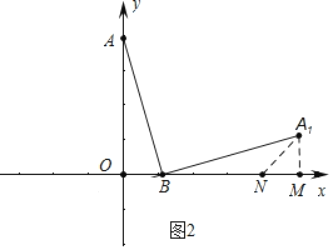
∵△ABO≌△BA1M,
∴OA=BM=ON,OB=A1M,
∴OB=MN=A1M,
∴△A1MN是等腰直角三角形,
∴∠A1NM=45°,
∴点A1在经过点N,与x轴的夹角为45°的直线上,
易知这条直线的解析式为y=x﹣4,
∴P1(x,y)是点A关于点B的“伴随点”,y与x之间的关系式为y=x﹣4;
(2)如图3中,
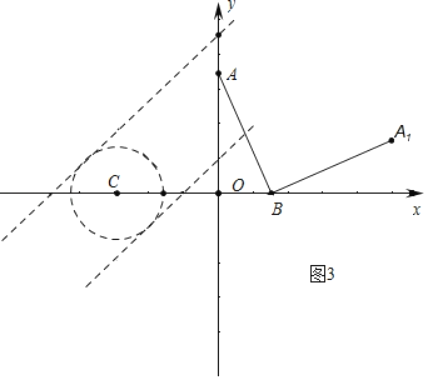
由(1)可知,A(0,m)关于B的“伴随点”A1(x,y),
y与x之间的关系式:y=x﹣m,
由题意可知,当直线y=x﹣m与⊙C有交点时,在⊙C上存在点A关于点B的“伴随点”,易知相切时m=±1,
观察图象可知,满足条件的m的范围为:m≤﹣1或m≥1.


科目:初中数学 来源: 题型:
【题目】如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°. 求小岛B到河边公路AD的距离.
(参考数据:sin37°≈ 0.60,cos37° ≈ 0.80,tan37° ≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动:探究与发现
定义:如图(1),四边形ABCD为矩形,△ADE和△BCF均为等腰直角三角形,∠AED=∠BFC=90°,点G、H分别为AB、CD的中点,连接EG、EH、FG、FH,分别与AD、BC交于点M、P、N、Q,我们把四边形PQNM叫做矩形ABCD的递推四边形.
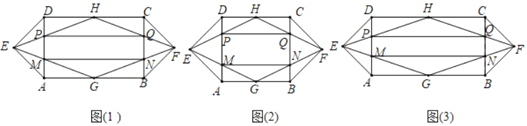
独立思考:
(1)求证:四边形PQNM矩形.
合作交流:
(2)解决完上述问题后,“兴趣”小组的同学们对正方形ABCD的递推四边形进行了探究,如图(2),他们猜想矩形PQNM的宽与长的比![]() .他们猜想的结论是否正确?请说明理由.
.他们猜想的结论是否正确?请说明理由.
发现问题:(3)在“兴趣”小组同学们的启发下,“实践”小组的同学们对宽与长的比为![]() 的矩形的递推四边形进行了探究,如图(3).他们提出如下问题:
的矩形的递推四边形进行了探究,如图(3).他们提出如下问题:
①在矩形ABCD中,若![]() ,则矩形PQNM的宽与长的比为_____;
,则矩形PQNM的宽与长的比为_____;
②在矩形ABCD中,若![]() ,则矩形PQNM的宽与长的比为______;
,则矩形PQNM的宽与长的比为______;
③在矩形ABCD中,若![]() ,则矩形PQNM的宽与长的比为______.
,则矩形PQNM的宽与长的比为______.
任务:请你完成“实践”小组提出的数学问题.(注:直接写出结果,不要求说理或证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为50000元,今年销售总额将比去年减少20%,每辆销售价比去年降低400元,若这两年卖出的数量相同.A,B两种型号车今年的进货和销售价格表:
A型车 | B型车 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
(1)求今年A型车每辆售价多少元?
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,求销售这批车获得的最大利润是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角坐标系中一条圆弧经过正方形网格的格点A(0,4)、B(4,4)、C(6,2)
(1)用直尺画出该圆弧所在圆的圆心M的位置,并标出M点的坐标;
(2)若D点的坐标为(7,0),想一想直线CD与⊙M有怎样的位置关系,并证明你的猜想.
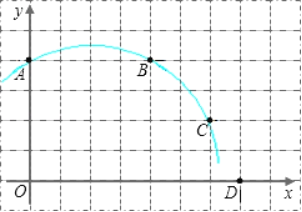
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
(3)在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将二次函数y=-(x-2)2+4(x≤4)的图象沿直线x=4翻折,翻折前后的图象组成一个新图象M,若直线y=b和图象M有四个交点,结合图象可知,b的取值范围是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
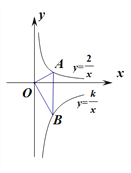
【题目】如图所示是一块含30°的直角三角板,直角顶点O位于坐标原点,斜边AB⊥x轴,顶点A在函数![]() (x>0)的图象上,顶点B在函数
(x>0)的图象上,顶点B在函数![]() (x>0)的图象上,∠ABO=30°,则k=_________.
(x>0)的图象上,∠ABO=30°,则k=_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com