
 ��ƽ��ֱ������ϵxOy�У�����D�ڵ�һ����������y=-x2-kx-��k-1����x�ύ��A��x1��0����B��x2��0�����㣨��A�ڵ�B����࣬OA��OB������y ���ڵ�C����x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10��
��ƽ��ֱ������ϵxOy�У�����D�ڵ�һ����������y=-x2-kx-��k-1����x�ύ��A��x1��0����B��x2��0�����㣨��A�ڵ�B����࣬OA��OB������y ���ڵ�C����x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10������ ��1�����������߶�Ӧ��һԪ���η�������֮���ϵ���Kֵ�����������ߣ��������㶥��D�ڵ�һ��������������߽���ʽ��
��2�����������������������P�����꣬���PQֱ�߽���ʽ�����������飬�����P��Q���꣬�����������빫ʽ��������������ζ�Ӧ�߶εij��������������������Σ����������R�����ꣻ
��3�����ֱ��BD����ʽ���߶�BD���ȣ�������֪BD=KN�������N��K���꣬���õ������������������M���ꣻ
��� �⣺��1����y=0��
-x2-kx-��k-1��=0��
�ࣨx-1��[x+��k-1��]=0��
��x=1��x=1-k��
��x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10��
��1+��1-k��2=10��
��ã�k=4����k=-2��
��k=4��������Ϊy=-x2-4x-3��
����D������Ϊ-2�����ڵ�һ���ޣ���ȥ��
��k=-2ʱ�������߽���ʽΪ��y=-x2+2x+3��
��������D��1��4����
�������߽���ʽΪ��y=-x2+2x+3��
��2���ɣ�1���ã�A��-1��0����B��3��0����C��0��3����
���߶�AB��ֱƽ����Ϊֱ��x=1��
�߶�BC�Ĵ�ֱƽ����Ϊֱ��y=x��
������P��1��1����
ֱ��AC����ʽΪ��y=3x+3��
��ֱ��PQ��y=kx+b�����루1��1����
��y=kx+1-k��
��y=0��x=$\frac{k-1}{k}$��
��R��$\frac{k-1}{k}$��0��
������ֱ��AC��QR
���Q��$\frac{2+k}{k-3}$��$\frac{6k-3}{k-3}$����
���ù��ɶ�����ã�
AC=$\sqrt{10}$��AB=4��AQ=$\sqrt{��-1-\frac{2+k}{k-3}��^{2}+��\frac{6k-3}{k-3}��^{2}}$����AR=$\frac{k-1}{k}$+1
����ARQ�ס�ABCʱ��
$\frac{AC}{AQ}$=$\frac{AB}{AR}$����ã�k=-1��
��R��2��0����
����ARQ�ס�ACBʱ��
$\frac{AC}{AR}=\frac{AB}{AQ}$�����k=-2��
��R��$\frac{3}{2}$��0����
��R������ΪR��$\frac{3}{2}$��0����R��2��0����
��3����ֱ��BD����ʽΪy=kx+b��
��B��3��0����D��1��4����
����ֱ�߽���ʽ�ã�k=-2��b=6��
��ֱ��BD����ʽΪy=-2x+6��
BD=$\sqrt{{4}^{2}+��3-1��^{2}}$=2$\sqrt{5}$��
���M��0��b����
��BM=BD=2$\sqrt{5}$��
��OM=$\sqrt{B{M}^{2}-O{B}^{2}}$=$\sqrt{20-9}$=$\sqrt{11}$��
��M��0��$\sqrt{11}$��
��BD=BMʱ�����������߶Գ��ԣ���M��y�Ḻ���ᣬ���������⣮
��BM=DMʱ��
$\sqrt{9+{b}^{2}}$=$\sqrt{1+��4-b��^{2}}$��
��ã�b=1��
��M��0��1����
������������M������0��1����0��$\sqrt{11}$����
���� ��Ŀ����Ķ��κ������ۺ�Ӧ�ã�ͨ���Զ��κ���һ�κ�������ʽ����⣬������������Σ�����ѧ������ۺ��������������Ŀ������ѣ�����ѹ���⣬�ʺ�ѧ������п�ѹ��ѵ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ������D�ǡ�O��һ�㣬��C�ǻ�AD���е㣬����AC��BD��AD��BC���ڵ�Q��
��ͼ��AB�ǡ�O��ֱ������D�ǡ�O��һ�㣬��C�ǻ�AD���е㣬����AC��BD��AD��BC���ڵ�Q���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
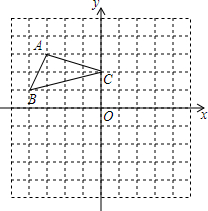 ����ֽ��ÿ��С�����εı߳�����1����λ���ȣ���ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��
����ֽ��ÿ��С�����εı߳�����1����λ���ȣ���ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | �� | �� | ||||||||||
| y | �� | �� |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a+2b=5ab | B�� | -2m+2m=0 | C�� | 5x2-x=5x | D�� | 4p3-p2=3p |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
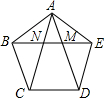 ��ͼ�����������ABCDE�У��Խ���AD��AC��EB�ֱ��ڵ�M��N��
��ͼ�����������ABCDE�У��Խ���AD��AC��EB�ֱ��ڵ�M��N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 90 | B�� | 80 | C�� | 70 | D�� | 60 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com