
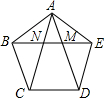
 如图,在正五边形ABCDE中,对角线AD、AC与EB分别交于点M、N.
如图,在正五边形ABCDE中,对角线AD、AC与EB分别交于点M、N.分析 (1)根据正五边形的性质得到AB=DE=AE,∠BAE=∠AED=108°,根据全等三角形的判定定理即可得到结论;
(2)根据正五边形的性质得到∠DAE=∠DAE,∠ADE=∠AEM=36°,推出△AME∽△AED,根据相似三角形的性质得到$\frac{AE}{AD}=\frac{AM}{AE}$,于是得到AE2=AD•AM,等量代换即可得到结论.
解答 证明:(1)∵五边形ABCDE是正五边形,
∴AB=DE=AE,∠BAE=∠AED=108°,
在△ABE与△EDA中,
$\left\{\begin{array}{l}{AB=AE}\\{∠BAE=∠AED}\\{AE=DE}\end{array}\right.$,
∴△ABE≌△EDA;
(2)∵∠DAE=∠DAE,∠ADE=∠AEM=36°,
∴△AME∽△AED,
∴$\frac{AE}{AD}=\frac{AM}{AE}$,
∴AE2=AD•AM,
∵AE=DE=DM,
∴DM2=AD•AM,
∴点M是AD的黄金分割点.
点评 本题考查了正五边形的性质、全等三角形的判定和性质,黄金分割,熟记正五边形的性质是解题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,顶点D在第一象限的抛物线y=-x2-kx-(k-1)与x轴交于A(x1,0)、B(x2,0)两点(点A在点B的左侧,OA<OB),交y 轴于点C,且x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10.
在平面直角坐标系xOy中,顶点D在第一象限的抛物线y=-x2-kx-(k-1)与x轴交于A(x1,0)、B(x2,0)两点(点A在点B的左侧,OA<OB),交y 轴于点C,且x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是李明同学在求阴影部分的面积时,列出的4个式子,其中错误的是( )
如图,是李明同学在求阴影部分的面积时,列出的4个式子,其中错误的是( )| A. | ab+(c-a)a | B. | ac+(b-a)a | C. | ab+ac-a2 | D. | bc+ac-a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{121}$=±11 | B. | ±$\sqrt{\frac{9}{25}}$=$\frac{3}{5}$ | C. | $\sqrt{(-\frac{1}{3})^{2}}$=-$\frac{1}{3}$ | D. | $\sqrt{0.16}$=0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com