
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:
“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.
例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
(1)已知点A(1,2),B(﹣3,1),P(0,t).
①若A,B,P三点的“矩面积”为12,求点P的坐标;
②直接写出A,B,P三点的“矩面积”的最小值.
(2)已知点E(4,0),F(0,2),M(m,4m),N(n, ![]() ),其中m>0,n>0.
),其中m>0,n>0.
①若E,F,M三点的“矩面积”为8,求m的取值范围;
②直接写出E,F,N三点的“矩面积”的最小值及对应n的取值范围.
【答案】(1)①点P 的坐标为(0,﹣1);②A,B,P三点的“矩面积”的最小值为4;
(2)①∴0<m≤![]() ;②E,F,N三点的“矩面积”的最小值为16,此时n的取值范围为4≤n≤8.
;②E,F,N三点的“矩面积”的最小值为16,此时n的取值范围为4≤n≤8.
【解析】试题分析:(1)①首先由题意:a=4,然后分别从①当t>2时,h=t-1,当t<1时,h=2-t,去分析求解即可求得答案;
②首先根据题意得:h的最小值为:1,继而求得A,B,P三点的“矩面积”的最小值.
(2)①由E,F,M三点的“矩面积”的最小值为8,可得a=4,h=2,即可得![]() ,继而求得m的取值范围;
,继而求得m的取值范围;
②分别从当n≤4时,a=4,h=![]() ,当4<n<8时,a=n,h=
,当4<n<8时,a=n,h=![]() ,,当n≥8时,a=n,h=2,去分析求解即可求得答案;
,,当n≥8时,a=n,h=2,去分析求解即可求得答案;
试题解析:
解:(1)由题意:a=4.
①当t>2时,h=t﹣1,
则4(t﹣1)=12,可得t=4,故点P的坐标为(0,4);
当t<1时,h=2﹣t,
则4(2﹣t)=12,可得t=﹣1,故点P 的坐标为(0,﹣1);
②∵根据题意得:h的最小值为:1,
∴A,B,P三点的“矩面积”的最小值为4;
(2)①∵E,F,M三点的“矩面积”为8,
∴a=4,h=2,
∴![]() .
.
∴0≤m≤![]() .
.
∵m>0,
∴0<m≤![]() ;
;
②∵当n≤4时,a=4,h=![]() ,此时S=ah=
,此时S=ah=![]() ,
,
∴当n=4时,取最小值,S=16;
当4<n<8时,a=n,h=![]() ,此时S=ah=16;
,此时S=ah=16;
当n≥8时,a=n,h=2,此时S=ah=2n,
∴当n=8时,取最小值,S=16;
∴E,F,N三点的“矩面积”的最小值为16,此时n的取值范围为4≤n≤8.


科目:初中数学 来源: 题型:
【题目】有这样一对数:一个数的数字排列完全颠倒过来就变成另一个数,简单地说就是顺序相反的两个数,我们把这样的一对数互称为反序数.比如:68的反序数是86,235的反序数是532,4056的反序数是6504.根据以上阅读材料,回答下列问题:
(1)已知一个三位数,其数位上的数字为连续的三个自然数,请写出满足条件的一对反序数 与 ,并求出原三位数与其反序数之差的绝对值 ;
(2)如果一个两位数等于其反序数与1的平均数,求这个两位数;
(3)若一个两位数在其中间插入一个数字![]() (
(![]() ,
,![]() 为整数),得到的这个三位数是原来两位数的9倍,请求出满足条件的两位数的反序数.
为整数),得到的这个三位数是原来两位数的9倍,请求出满足条件的两位数的反序数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是确定事件的是( )
A. 射击运动员只射击1次,就命中靶心
B. 打开电视,正在播放新闻
C. 任意一个三角形,它的内角和等于180°
D. 抛一枚质地均匀的正方体骰子,朝上一面的点数为6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解七年级学生最喜爱的球类运动情况,从中随机抽取部分学生进行调查统计,调查项目为篮球、乒乓球、足球和排球(每个被抽查的学生必须选择且只能选择其中一个调查项目),对调查结果绘制成如下不完整的统计图: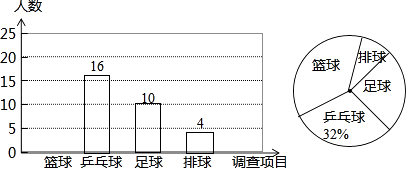
根据以上统计图提供的信息,回答下列问题:
(1)求本次抽样调查的样本容量;
(2)请补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在你的班里做一项有关师生关系的调查,分四个方面:①自由平等的师生关系②既注重师道尊严,又注重平等的师生关系③传统的尊师爱生的关系④不太协调的关系,请你统计出四个方面的人数,回答以下问题.
①列出表格,并作出相应的统计图.
②任取一名同学,他与老师之间的关系是自由平等的师生关系,是哪一种事件?可能性约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P(3a,a)是反比例函数y= ![]() (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y= ![]()
B.y= ![]()
C.y= ![]()
D.y= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
【发现】
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
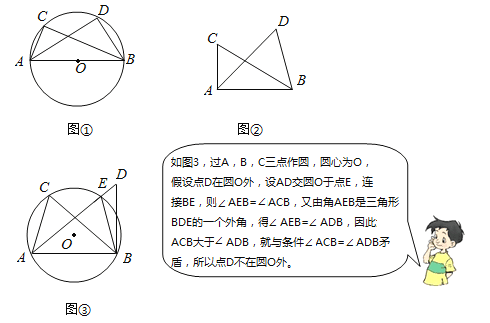
【思考】
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?
请证明点D也不在⊙O内.
【应用】
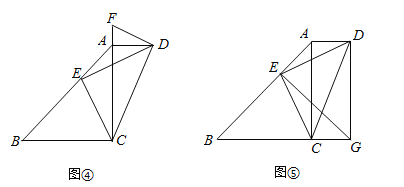
利用【发现】和【思考】中的结论解决问题:若四边形ABCD中,AD∥BC,∠CAD=90°,点E在边AB上,CE⊥DE.
(1)作∠ADF=∠AED,交CA的延长线于点F(如图④),求证:DF为Rt△ACD的外接圆的切线;
(2)如图⑤,点G在BC的延长线上,∠BGE=∠BAC,已知sin∠AED=![]() ,AD=1,求DG的长.
,AD=1,求DG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com