
���� ��1�����ݾ���ֵ�Լ�ż�η��ķǸ��Լ��ɵó�����a��b��һԪһ�η��̣���֮���ɵó�a��b��ֵ��
��2����x���A��B�������2����λ���ȣ����ݵ�A��B���˶��ҳ�x����A��B��Ӧ�������ٸ����������2����λ���ȼ��ɵó�����x�ĺ�����ֵ���ŵ�һԪһ�η��̣���֮���ɵó����ۣ�
��3���ҳ����˶�ʱ��Ϊt��ʱ����M��N��Ӧ���������NO���е�ΪP�����ҳ�PO��AM����������ɵó����ۣ�
��� �⣺��1����|a+6|+��b-12��2=0��
��a+6=0��b-12=0��
��a=-6��b=12��
��2����x���A��B�������2����λ���ȣ�
��������ã�|��2x+12��-��3x-6��|=2��
��ã�x1=16��x2=20��
��16���20���A��B�������2����λ���ȣ�
��3�����˶�ʱ��Ϊt��ʱ����M��Ӧ����Ϊt-6����N��Ӧ����Ϊ2t+12��
��NO���е�ΪP��
��PO=$\frac{1}{2}$NO=t+6��AM=t-6-��-6��=t��
��PO-AM=t+6-t=6��
��PO-AMΪ��ֵ6��
���� ���⿼����һԪһ�η��̵�Ӧ�á����ᡢż�η�������ֵ�ķǸ����Լ������ľ��빫ʽ������Ĺؼ�����1�����ݾ���ֵ�Լ�ż�η��ķǸ������a��b�ľ���ֵ����2�����������ľ��빫ʽ�ҳ�����x�ĺ�����ֵ���ŵ�һԪһ�η��̣���3���ҳ��˶�ʱ��Ϊt��ʱPO��AM��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3.97��1010 | B�� | 0.379��1013 | C�� | 3.79��1010 | D�� | 3.79��1012 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
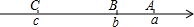 ��ͼ����֪������A��B��C�����Ӧ�����ֱ�Ϊa��b��c������|a-b|+|c-b|+|c-a|=2a-2c��
��ͼ����֪������A��B��C�����Ӧ�����ֱ�Ϊa��b��c������|a-b|+|c-b|+|c-a|=2a-2c���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
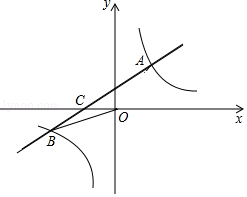 ��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=ax+b��a��b�dz�������a��0����ͼ���뷴��������$y=\frac{k}{x}$��k�dz�������k��0����ͼ����һ���������ڵ�A��B���㣬��x�ύ�ڵ�C����A������Ϊ��2��m������B������Ϊ��n��-2����tan��BOC=$\frac{2}{5}$��
��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=ax+b��a��b�dz�������a��0����ͼ���뷴��������$y=\frac{k}{x}$��k�dz�������k��0����ͼ����һ���������ڵ�A��B���㣬��x�ύ�ڵ�C����A������Ϊ��2��m������B������Ϊ��n��-2����tan��BOC=$\frac{2}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com