【题目】某服装店出售某品牌的棉衣，进价为100元/件，当售价为150元/件时，平均每天可卖30件；为了尽快减少库存迎接“元旦”的到来，商店决定降价销售，增加利润，经调查每件降价5元，则每天可多卖10件，现要想平均每天获利2000元，且让顾客得到实惠，那么每件棉衣应降价多少元？
阅读快车系列答案科目：初中数学 来源： 题型：
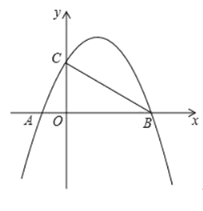
【题目】如图，已知抛物线yax2bxc(a0)经过A(1,0)，B(4,0)，C(0,2)三点．
（1）求这条抛物线和直线BC的解析式；
（2）E为抛物线上一动点，是否存在点E，使以A、B、E为顶点的三角形与COB相似？若存在，试求出点E的坐标；若不存在，请说明理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线
经过B、C两点，顶点D在正方形内部．
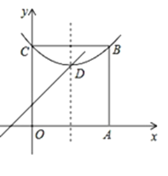
（1）直接写出点D（m，n）所有的特征线 ;
（2）若点D有一条特征线是y=x+1，求此抛物线的解析式；
（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于y轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？
查看答案和解析>>
科目：初中数学 来源： 题型：
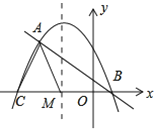
【题目】在平面直角坐标系中，我们定义直线y=ax-a为抛物线y=ax2+bx+c（a、b、c为常数，a≠0）的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在y轴上的三角形为其“梦想三角形”．已知抛物线y=-
与其“梦想直线”交于A、B两点（点A在点B的左侧），与x轴负半轴交于点C．
（1）填空：该抛物线的“梦想直线”的解析式为______，点A的坐标为______，点B的坐标为______．
（2）如图，点M为线段CB上一动点，将△ACM以AM所在直线为对称轴翻折，点C的对称点为N，若△AMN为该抛物线的“梦想三角形”，求点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程．
已知：如图，⊙O及⊙O上一点P．
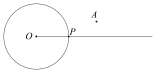
求作：过点P的⊙O的切线．
作法：如图，作射线OP；
① 在直线OP外任取一点A，以A为圆心，AP为半径作⊙A，与射线OP交于另一点B；
②连接并延长BA与⊙A交于点C；
③作直线PC；
则直线PC即为所求．根据小元设计的尺规作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的证明：
证明：∵ BC是⊙A的直径，
∴ ∠BPC=90° （填推理依据）．
∴ OP⊥PC．
又∵ OP是⊙O的半径，
∴ PC是⊙O的切线 （填推理依据）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店销售一种商品，经市场调査发现，该商品的周销售量y（件）是售价x（元/件）的一次函数．其售价、周销售量、周销售利润w（元）的三组对应值如表：
售价x（元/件） | 50 | 60 | 80 |
周销售量y（件） | 100 | 80 | 40 |
周销售利润w（元） | 1000 | 1600 | 1600 |
注：周销售利润＝周销售量×（售价﹣进价）
（1）求y关于x的函数解析式_____；
（2）当售价是_____元/件时，周销售利润最大．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知ABCD中，∠ABC＝60°，AB＝4，BC＝m，E为BC边上的动点，连结AE，作点B关于直线AE的对称点F．
（1）若m＝6，①当点F恰好落在∠BCD的平分线上时，求BE的长；
②当E、C重合时，求点F到直线BC的距离；
（2）当点F到直线BC的距离d满足条件：2
﹣2≤d≤2+4，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
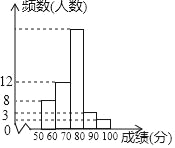
【题目】（7分）某中学1000名学生参加了”环保知识竞赛“，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取整数，满分为100分）作为样本进行统计，并制作了如图频数分布表和频数分布直方图（不完整且局部污损，其中“■”表示被污损的数据）．请解答下列问题：
成绩分组 | 频数 | 频率 |
50≤x＜60 | 8 | 0.16 |
60≤x＜70 | 12 | a |
70≤x＜80 | ■ | 0.5 |
80≤x＜90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
（1）写出a，b，c的值；
（2）请估计这1000名学生中有多少人的竞赛成绩不低于70分；
（3）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取两名同学参加环保知识宣传活动，求所抽取的2名同学来自同一组的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
