
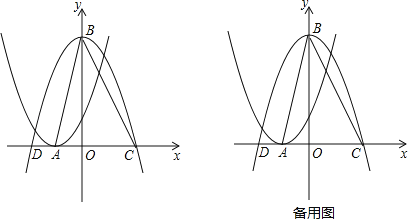
°ĺŐ‚ńŅ°Ņ»ÁÕľňý ĺ£¨Ĺę∂ĢīőļĮ ży=x2+2x+1ĶńÕľŌů—ōx÷Š∑≠’Ř£¨»ĽļůŌÚ”“∆Ĺ“∆1łŲĶ•őĽ£¨‘ŔŌÚ…Ō∆Ĺ“∆4łŲĶ•őĽ£¨Ķ√ĶĹ∂ĢīőļĮ ży=ax2+bx+cĶńÕľŌů£ģļĮ ży=x2+2x+1ĶńÕľŌůĶń∂•Ķ„ő™Ķ„A£ģļĮ ży=ax2+bx+cĶńÕľŌůĶń∂•Ķ„ő™Ķ„B£¨ļÕx÷ŠĶńĹĽĶ„ő™Ķ„C£¨D£®Ķ„DőĽ”ŕĶ„CĶń◊ů≤ŗ£©£ģ
£®1£©«ůļĮ ży=ax2+bx+cĶńĹ‚őŲ Ĺ£Ľ
£®2£©ī”Ķ„A£¨C£¨D»żłŲĶ„÷–»ő»°ŃĹłŲĶ„ļÕĶ„BĻĻ‘ž»żĹ«–ő£¨«ůĻĻ‘žĶń»żĹ«–ő «Ķ»—Ł»żĹ«–őĶńłŇ¬ £Ľ
£®3£©»ŰĶ„M «ŌŖ∂őBC…ŌĶń∂ĮĶ„£¨Ķ„N «°ųABC»żĪŖ…ŌĶń∂ĮĶ„£¨ «∑Ůīś‘ŕ“‘AMő™–ĪĪŖĶńRt°ųAMN£¨ Ļ°ųAMNĶń√śĽżő™°ųABC√śĽżĶń![]() £Ņ»Űīś‘ŕ£¨«ůtan°ŌMANĶń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
£Ņ»Űīś‘ŕ£¨«ůtan°ŌMANĶń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©Ĺ‚őŲ Ĺő™y=©Āx2+4£Ľ£®2£©ĻĻ‘žĶń»żĹ«–ő «Ķ»—Ł»żĹ«–őĶńłŇ¬ «![]() £Ľ£®3£©īś‘ŕ£¨tan°ŌMANĶń÷Ķő™1ĽÚ4ĽÚ
£Ľ£®3£©īś‘ŕ£¨tan°ŌMANĶń÷Ķő™1ĽÚ4ĽÚ![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ£®1£©ņŻ”√Ňš∑Ĺ∑®Ķ√ĶĹy=x2+2x+1=£®x+1£©2£¨»Ľļůłýĺ›Ň◊őÔŌŖĶńĪšĽĽĻś¬…«ůĹ‚£Ľ
£®2£©ņŻ”√∂•Ķ„ Ĺy=£®x+1£©2Ķ√ĶĹA£®©Ā1£¨0£©£¨Ĺ‚∑Ĺ≥Ő©Āx2+4=0Ķ√D£®©Ā2£¨0£©£¨C£®2£¨0£©“◊Ķ√B£®0£¨4£©£¨Ń–ĺŔ≥Ųňý”–Ķń»żĹ«–ő£¨‘Ŕľ∆ň„≥ŲAC=3£¨AD=1£¨CD=4£¨AB=![]() £¨BC=2
£¨BC=2![]() £¨BD=2
£¨BD=2![]() £¨»Ľļůłýĺ›Ķ»—Ł»żĹ«–őĶńŇ–∂®∑Ĺ∑®ļÕłŇ¬ Ļę Ĺ«ůĹ‚£Ľ
£¨»Ľļůłýĺ›Ķ»—Ł»żĹ«–őĶńŇ–∂®∑Ĺ∑®ļÕłŇ¬ Ļę Ĺ«ůĹ‚£Ľ
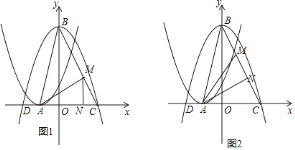
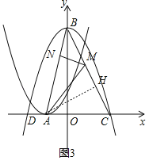
£®3£©“◊Ķ√BCĶńĹ‚őŲ «ő™y=©Ā2x+4£¨S°ųABC=6£¨MĶ„Ķń◊ÝĪÍő™£®m£¨©Ā2m+4£©£®0°‹m°‹2£©£¨Ő÷¬Ř£ļĘŔĶĪNĶ„‘ŕAC…Ō£¨»ÁÕľ1£¨ņŻ”√√śĽżĻę ĹĶ√ĶĹ![]() £®m+1£©£®©Ā2m+4£©=2£¨Ĺ‚Ķ√m1=0£¨m2=1£¨ĶĪm=0 Ī£¨«ů≥ŲAN=1£¨MN=4£¨‘ŔņŻ”√’ż«–∂®“Śľ∆ň„tan°ŌMACĶń÷Ķ£ĽĶĪm=1 Ī£¨ľ∆ň„≥ŲAN=2£¨MN=2£¨‘ŔņŻ”√’ż«–∂®“Śľ∆ň„tan°ŌMACĶń÷Ķ£ĽĘŕĶĪNĶ„‘ŕBC…Ō£¨»ÁÕľ2£¨Ō»ņŻ”√√śĽż∑®ľ∆ň„≥ŲAN=
£®m+1£©£®©Ā2m+4£©=2£¨Ĺ‚Ķ√m1=0£¨m2=1£¨ĶĪm=0 Ī£¨«ů≥ŲAN=1£¨MN=4£¨‘ŔņŻ”√’ż«–∂®“Śľ∆ň„tan°ŌMACĶń÷Ķ£ĽĶĪm=1 Ī£¨ľ∆ň„≥ŲAN=2£¨MN=2£¨‘ŔņŻ”√’ż«–∂®“Śľ∆ň„tan°ŌMACĶń÷Ķ£ĽĘŕĶĪNĶ„‘ŕBC…Ō£¨»ÁÕľ2£¨Ō»ņŻ”√√śĽż∑®ľ∆ň„≥ŲAN=![]() £¨‘Ŕłýĺ›»żĹ«–ő√śĽżĻę Ĺľ∆ň„≥ŲMN=
£¨‘Ŕłýĺ›»żĹ«–ő√śĽżĻę Ĺľ∆ň„≥ŲMN=![]() £¨»ĽļůņŻ”√’ż«–∂®“Śľ∆ň„tan°ŌMACĶń÷Ķ£ĽĘŘĶĪNĶ„‘ŕAB…Ō£¨»ÁÕľ3£¨◊ųAH°ÕBC”ŕH£¨…ŤAN=t£¨‘ÚBN=
£¨»ĽļůņŻ”√’ż«–∂®“Śľ∆ň„tan°ŌMACĶń÷Ķ£ĽĘŘĶĪNĶ„‘ŕAB…Ō£¨»ÁÕľ3£¨◊ųAH°ÕBC”ŕH£¨…ŤAN=t£¨‘ÚBN=![]() ©Āt£¨”…ĘŕĶ√AH=
©Āt£¨”…ĘŕĶ√AH=![]() £¨ņŻ”√ĻīĻ…∂®ņŪŅ…ľ∆ň„≥ŲBH=
£¨ņŻ”√ĻīĻ…∂®ņŪŅ…ľ∆ň„≥ŲBH=![]() £¨÷§√ų°ųBNM°◊°ųBHA£¨ņŻ”√Ōŗň∆Ī»Ņ…Ķ√ĶĹMN=
£¨÷§√ų°ųBNM°◊°ųBHA£¨ņŻ”√Ōŗň∆Ī»Ņ…Ķ√ĶĹMN=![]() £¨ņŻ”√»żĹ«–ő√śĽżĻę ĹĶ√ĶĹ
£¨ņŻ”√»żĹ«–ő√śĽżĻę ĹĶ√ĶĹ![]() £®
£®![]() ©Āt£©
©Āt£©![]() =2£¨łýĺ›īň∑Ĺ≥Ő√Ľ”– Ķ żĹ‚Ņ…Ň–∂ŌĶ„N‘ŕAB…Ō≤Ľ∑ŻļŌŐűľĢ£¨ī”∂ÝĶ√ĶĹtan°ŌMANĶń÷Ķő™1ĽÚ4ĽÚ
=2£¨łýĺ›īň∑Ĺ≥Ő√Ľ”– Ķ żĹ‚Ņ…Ň–∂ŌĶ„N‘ŕAB…Ō≤Ľ∑ŻļŌŐűľĢ£¨ī”∂ÝĶ√ĶĹtan°ŌMANĶń÷Ķő™1ĽÚ4ĽÚ![]() £ģ
£ģ
£®1£©y=x2+2x+1=£®x+1£©2ĶńÕľŌů—ōx÷Š∑≠’Ř£¨Ķ√y=©Ā£®x+1£©2£¨
į—y=©Ā£®x+1£©2ŌÚ”“∆Ĺ“∆1łŲĶ•őĽ£¨‘ŔŌÚ…Ō∆Ĺ“∆4łŲĶ•őĽ£¨Ķ√y=©Āx2+4£¨
°ŗňý«ůĶńļĮ ży=ax2+bx+cĶńĹ‚őŲ Ĺő™y=©Āx2+4£Ľ
£®2£©°Ŗy=x2+2x+1=£®x+1£©2£¨
°ŗA£®©Ā1£¨0£©£¨
ĶĪy=0 Ī£¨©Āx2+4=0£¨Ĺ‚Ķ√x=°ņ2£¨‘ÚD£®©Ā2£¨0£©£¨C£®2£¨0£©£Ľ
ĶĪx=0 Ī£¨y=©Āx2+4=4£¨‘ÚB£®0£¨4£©£¨
ī”Ķ„A£¨C£¨D»żłŲĶ„÷–»ő»°ŃĹłŲĶ„ļÕĶ„BĻĻ‘ž»żĹ«–őĶń”–£ļ°ųACB£¨°ųADB£¨°ųCDB£¨
°ŖAC=3£¨AD=1£¨CD=4£¨AB=![]() £¨BC=2
£¨BC=2![]() £¨BD=2
£¨BD=2![]() £¨
£¨
°ŗ°ųBCDő™Ķ»—Ł»żĹ«–ő£¨
°ŗĻĻ‘žĶń»żĹ«–ő «Ķ»—Ł»żĹ«–őĶńłŇ¬ =![]() £Ľ
£Ľ
£®3£©īś‘ŕ£¨
“◊Ķ√BCĶńĹ‚őŲ «ő™y=©Ā2x+4£¨S°ųABC=![]() ACOB=
ACOB=![]() °Ń3°Ń4=6£¨
°Ń3°Ń4=6£¨
MĶ„Ķń◊ÝĪÍő™£®m£¨©Ā2m+4£©£®0°‹m°‹2£©£¨
ĘŔĶĪNĶ„‘ŕAC…Ō£¨»ÁÕľ1£¨
°ŗ°ųAMNĶń√śĽżő™°ųABC√śĽżĶń![]() £¨
£¨
°ŗ![]() £®m+1£©£®©Ā2m+4£©=2£¨Ĺ‚Ķ√m1=0£¨m2=1£¨
£®m+1£©£®©Ā2m+4£©=2£¨Ĺ‚Ķ√m1=0£¨m2=1£¨
ĶĪm=0 Ī£¨MĶ„Ķń◊ÝĪÍő™£®0£¨4£©£¨N£®0£¨0£©£¨‘ÚAN=1£¨MN=4£¨
°ŗtan°ŌMAC=![]() =4£Ľ
=4£Ľ
ĶĪm=1 Ī£¨MĶ„Ķń◊ÝĪÍő™£®1£¨2£©£¨N£®1£¨0£©£¨‘ÚAN=2£¨MN=2£¨
°ŗtan°ŌMAC=![]() =1£Ľ
=1£Ľ
ĘŕĶĪNĶ„‘ŕBC…Ō£¨»ÁÕľ2£¨
BC=![]() =2
=2![]() £¨
£¨
°Ŗ![]() BCAN=
BCAN=![]() ACBC£¨Ĺ‚Ķ√AN=
ACBC£¨Ĺ‚Ķ√AN=![]() £¨
£¨
°ŖS°ųAMN=![]() ANMN=2£¨
ANMN=2£¨
°ŗMN=![]() =
=![]() £¨
£¨
°ŗ°ŌMAC=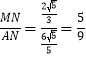 £Ľ
£Ľ
ĘŘĶĪNĶ„‘ŕAB…Ō£¨»ÁÕľ3£¨◊ųAH°ÕBC”ŕH£¨…ŤAN=t£¨‘ÚBN=![]() ©Āt£¨
©Āt£¨
”…ĘŕĶ√AH=![]() £¨‘ÚBH=
£¨‘ÚBH=![]() £¨
£¨
°Ŗ°ŌNBG=°ŌHBA£¨
°ŗ°ųBNM°◊°ųBHA£¨
°ŗ![]() £¨ľī
£¨ľī![]() £¨
£¨
°ŗMN=![]() £¨
£¨
°Ŗ![]() ANMN=2£¨
ANMN=2£¨
ľī![]() £®
£®![]() ©Āt£©
©Āt£©![]() =2£¨
=2£¨
’ŻņŪĶ√3t2©Ā3![]() t+14=0£¨°ų=£®©Ā3
t+14=0£¨°ų=£®©Ā3![]() £©2©Ā4°Ń3°Ń14=©Ā15£ľ0£¨∑Ĺ≥Ő√Ľ”– Ķ żĹ‚£¨
£©2©Ā4°Ń3°Ń14=©Ā15£ľ0£¨∑Ĺ≥Ő√Ľ”– Ķ żĹ‚£¨
°ŗĶ„N‘ŕAB…Ō≤Ľ∑ŻļŌŐűľĢ£¨
◊Ř…Ōňý Ų£¨tan°ŌMANĶń÷Ķő™1ĽÚ4ĽÚ![]() £ģ
£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņňś◊Ň–ŇŌĘľľ űĶń—ł√Õ∑Ę’Ļ£¨»ň√«»•…Ő≥°ĻļőÔĶń÷ßł∂∑Ĺ ĹłŁľ”∂ŗ—ý°ĘĪ„Ĺ›£ģń≥–£ ż—ß–ň»§–°◊ť…Ťľ∆Ńň“Ľ∑›Ķų≤ťő ĺŪ£¨“™«ů√Ņ»ň—°«“÷Ľ—°“Ľ÷÷ń„◊ÓŌ≤Ľ∂Ķń÷ßł∂∑Ĺ Ĺ£ģŌ÷ĹęĶų≤ťĹŠĻŻĹÝ––Õ≥ľ∆≤ĘĽś÷∆≥…»ÁŌ¬ŃĹ∑ý≤ĽÕÍ’ŻĶńÕ≥ľ∆Õľ£¨«ŽĹŠļŌÕľ÷–ňýłÝĶń–ŇŌĘĹ‚īūŌ¬Ń–ő Ő‚£ļ
£®1£©’‚īőĽÓ∂ĮĻ≤Ķų≤ťŃň°° °°»ň£Ľ‘ŕ…»–őÕ≥ľ∆Õľ÷–£¨ĪŪ ĺ°į÷ßł∂Ī¶°Ī÷ßł∂Ķń…»–ő‘≤–ńĹ«Ķń∂» żő™°° °°£Ľ
£®2£©ĹęŐű–őÕ≥ľ∆Õľ≤Ļ≥šÕÍ’Ż£ģĻŘ≤žīňÕľ£¨÷ßł∂∑Ĺ ĹĶń°į÷ŕ ż°Ī «°į°° °°°Ī£Ľ
£®3£©‘ŕ“ĽīőĻļőÔ÷–£¨–°√ųļÕ–°ŃŃ∂ľŌŽī”°įőĘ–Ň°Ī°Ę°į÷ßł∂Ī¶°Ī°Ę°į“Ý––Ņ®°Ī»ż÷÷÷ßł∂∑Ĺ Ĺ÷–—°“Ľ÷÷∑Ĺ ĹĹÝ––÷ßł∂£¨«Ž”√Ľ≠ ų◊īÕľĽÚŃ–ĪŪłŮĶń∑Ĺ∑®£¨«ů≥ŲŃĹ»ň«°ļ√—°‘ŮÕ¨“Ľ÷÷÷ßł∂∑Ĺ ĹĶńłŇ¬ £ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ…Ť÷–—ß…ķŐŚ÷ Ĺ°ŅĶ◊ŘļŌ∆ņ∂®≥…ľ®ő™x∑÷£¨¬ķ∑÷ő™100∑÷£ģĻś∂®£ļ85°‹x°‹100ő™Aľ∂£¨75°‹x£ľ85ő™Bľ∂£¨60°‹x£ľ75ő™Cľ∂£¨x£ľ60ő™Dľ∂£ģŌ÷ňśĽķ≥ť»°ł£ļ£÷–—ß≤Ņ∑÷—ß…ķĶń◊ŘļŌ∆ņ∂®≥…ľ®£¨’ŻņŪĽś÷∆≥…»ÁŌ¬ŃĹ∑ý≤ĽÕÍ’ŻĶńÕ≥ľ∆Õľ£ģ«Žłýĺ›Õľ÷–Ķń–ŇŌĘ£¨Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
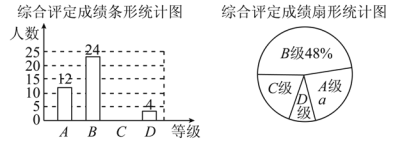
(1)‘ŕ’‚īőĶų≤ť÷–£¨“ĽĻ≤≥ť»°Ńň________√Ż—ß…ķ£¨a£Ĺ________%£Ľ
(2)≤Ļ»ęŐű–őÕ≥ľ∆Õľ£Ľ
(3)…»–őÕ≥ľ∆Õľ÷–Cľ∂∂‘”¶Ķń‘≤–ńĹ«ő™________∂»£Ľ
(4)»Űł√–£Ļ≤”–2 000√Ż—ß…ķ£¨«Žń„Ļņľ∆ł√–£Dľ∂—ß…ķ”–∂ŗ…Ŕ√Ż£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ–¬∂®“Ś£ļ∂‘”ŕĻō”ŕxĶń“ĽīőļĮ ży=kx+b£®k°Ŕ0£©£¨ő“√«≥∆ļĮ ży=![]() ő™“ĽīőļĮ ży=kx+b(k°Ŕ0)ĶńmĪšļĮ ż(∆š÷–mő™≥£ ż).
ő™“ĽīőļĮ ży=kx+b(k°Ŕ0)ĶńmĪšļĮ ż(∆š÷–mő™≥£ ż).
ņż»Á:∂‘”ŕĻō”ŕxĶń“ĽīőļĮ ży=x+4Ķń3ĪšļĮ żő™y=![]()
(1)Ļō”ŕxĶń“ĽīőļĮ ży=-x+1Ķń2ĪšļĮ żő™![]() ,‘ÚĶĪx=4 Ī£¨
,‘ÚĶĪx=4 Ī£¨![]() = ;
= ;
(2)Ļō”ŕxĶń“ĽīőļĮ ży=x+2Ķń1ĪšļĮ żő™![]() ,Ļō”ŕxĶń“ĽīőļĮ ży=-
,Ļō”ŕxĶń“ĽīőļĮ ży=-![]() x-2Ķń-1ĪšļĮ żő™
x-2Ķń-1ĪšļĮ żő™![]() ,«ůļĮ ż
,«ůļĮ ż![]() ļÕļĮ ż
ļÕļĮ ż![]() ĶńĹĽĶ„◊ÝĪÍ;
ĶńĹĽĶ„◊ÝĪÍ;
(3)Ļō”ŕxĶń“ĽīőļĮ ży=2x+2Ķń1ĪšļĮ żő™![]() ,Ļō”ŕxĶń“ĽīőļĮ ży=
,Ļō”ŕxĶń“ĽīőļĮ ży=![]() x-1£¨ĶńmĪšļĮ żő™
x-1£¨ĶńmĪšļĮ żő™![]() .
.
ĘŔĶĪ-3°‹x°‹3 Ī£¨ļĮ ż![]() Ķń»°÷Ķ∑∂őß « (÷ĪĹ”–ī≥Ųīūįł):
Ķń»°÷Ķ∑∂őß « (÷ĪĹ”–ī≥Ųīūįł):
Ęŕ»ŰļĮ ż![]() ļÕļĮ ż
ļÕļĮ ż![]() ”–«“ĹŲ”–ŃĹłŲĹĽĶ„£¨‘ÚmĶń»°÷Ķ∑∂őß « (÷ĪĹ”–ī≥Ųīūįł).
”–«“ĹŲ”–ŃĹłŲĹĽĶ„£¨‘ÚmĶń»°÷Ķ∑∂őß « (÷ĪĹ”–ī≥Ųīūįł).
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥…Ő≥°ő™∑ĹĪ„ŌŻ∑—’ŖĻļőÔ£¨◊ľĪłĹę‘≠ņīĶńĹ◊Ő› Ĺ◊‘∂Į∑ŲŐ›łń‘ž≥…–Ī∆¬ Ĺ◊‘∂Į∑ŲŐ›£ģ»ÁÕľňý ĺ£¨“—÷™‘≠Ĺ◊Ő› Ĺ◊‘∂Į∑ŲŐ›AB≥§ő™10m£¨∆¬Ĺ«°ŌABDő™30°„£Ľłń‘žļůĶń–Ī∆¬ Ĺ◊‘∂Į∑ŲŐ›Ķń∆¬Ĺ«°ŌACBő™15°„£¨«Žń„ľ∆ň„łń‘žļůĶń–Ī∆¬ Ĺ◊‘∂Į∑ŲŐ›ACĶń≥§∂»£¨£®ĹŠĻŻĺę»∑ĶĹ0£ģlm£ģő¬‹įŐŠ ĺ£ļsin15°„°÷0.26£¨cosl5°„°÷0.97£¨tan15°„°÷0.27£©
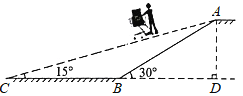
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ’ż∑Ĺ–őABCD÷–£¨∂‘Ĺ«ŌŖAC£¨BDĹĽ”ŕĶ„0£¨ĻżĶ„0Ķń÷ĪŌŖ∑÷ĪūĹĽĪŖAD£¨BC”ŕĶ„E£¨F£¨EF=6£ģ‘ÚAE2+BF2Ķń÷Ķő™£® £©
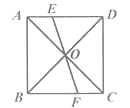
A. 9 B. 16 C. 18 D. 36
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨ĻżĶ„0Ķń÷ĪŌŖABĹĽ∑īĪ»ņżļĮ ży=![]() ĶńÕľŌů”ŕĶ„A£¨B£¨Ķ„c‘ŕ∑īĪ»ņżļĮ ży=
ĶńÕľŌů”ŕĶ„A£¨B£¨Ķ„c‘ŕ∑īĪ»ņżļĮ ży= ![]() (x>0)ĶńÕľŌů…Ō£¨Ń¨ĹŠCA£¨CB£¨ĶĪCA=CB«“cos°ŌCAB=
(x>0)ĶńÕľŌů…Ō£¨Ń¨ĹŠCA£¨CB£¨ĶĪCA=CB«“cos°ŌCAB= ![]() Ī£¨k1£¨k2”¶¬ķ◊„Ķń żŃŅĻōŌĶ «£® £©
Ī£¨k1£¨k2”¶¬ķ◊„Ķń żŃŅĻōŌĶ «£® £©
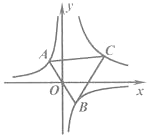
A. k2=2kl B. k2=-2k1 C. k2=4k1 D. k2=-4k1
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ°į ģ“Ľ°ĪĽ∆Ĺū÷‹∆ŕľš£¨ń≥ –‘ŕ![]() Őž÷–Õ‚≥Ų¬√”őĶń»ň żĪšĽĮ»ÁŌ¬ĪŪ£®’ż żĪŪ ĺĪ»«į“ĽŐž∂ŗĶń»ň ż£¨łļ żĪŪ ĺĪ»«į“ĽŐž…ŔĶń»ň ż£©
Őž÷–Õ‚≥Ų¬√”őĶń»ň żĪšĽĮ»ÁŌ¬ĪŪ£®’ż żĪŪ ĺĪ»«į“ĽŐž∂ŗĶń»ň ż£¨łļ żĪŪ ĺĪ»«į“ĽŐž…ŔĶń»ň ż£©
»’∆ŕ |
|
|
|
|
|
|
|
»ň żĪšĽĮ£®ÕÚ»ň£© |
|
|
|
|
|
|
|
£®1£©»Ű![]() ‘¬
‘¬![]() »’Õ‚≥Ų¬√”ő»ň żő™
»’Õ‚≥Ų¬√”ő»ň żő™![]() £¨ń«√ī
£¨ń«√ī![]() ‘¬
‘¬![]() »’Õ‚≥Ų¬√”őĶń»ň ż «∂ŗ…Ŕ£Ņ
»’Õ‚≥Ų¬√”őĶń»ň ż «∂ŗ…Ŕ£Ņ
£®2£©«ŽŇ–∂Ō∆ŖŐžńŕÕ‚≥Ų¬√”ő»ň ż◊Ó∂ŗĶń «ńńŐž£Ņ◊Ó…ŔĶń «ńńŐž£ŅňŁ√«Ōŗ≤Ó∂ŗ…Ŕ£Ņ
£®3£©»ÁĻŻ◊Ó∂ŗ“ĽŐž”–≥Ų”ő»ň ż![]() ÕÚ»ň£¨ń«√ī»Ű
ÕÚ»ň£¨ń«√ī»Ű![]() ‘¬
‘¬![]() »’Õ‚≥Ų¬√”őĶń”–∂ŗ…Ŕ»ň£Ņ
»’Õ‚≥Ų¬√”őĶń”–∂ŗ…Ŕ»ň£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥ –Ļ≤”–“Ľ÷–°Ę∂Ģ÷–°Ę»ż÷–Ķ»3ňýłŖ÷–£¨”–“ĽŐžňý”–łŖ∂Ģ—ß…ķ≤őľ”Ńň“Ľīő ż—ß≤‚ ‘£¨‘ńĺŪļůņŌ ¶√«∂‘Ķŕ10Ő‚ĹÝ––Ńň∑÷őŲ£¨į—√ŅłŲ—ß…ķĶńĹ‚īū«ťŅŲĻťĹŠő™Ō¬Ń–ňńņŗ«ťŅŲ÷ģ“Ľ£ļA(łŇńÓīŪőů)£¨B(ľ∆ň„īŪőů)£¨C(ĽýĪĺ’ż»∑)£¨D(Õͻ꒿»∑)£ģłų–£≥ŲŌ÷’‚ňńņŗ«ťŅŲĶń»ň ż’ľĪĺ–£łŖ∂Ģ—ß…ķ żĶńįŔ∑÷Ī»ľŻŌ¬√śĶńŐű–őÕ≥ľ∆Õľ£ļ
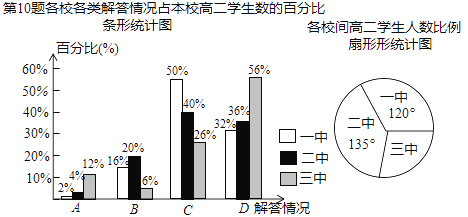
“—÷™“Ľ÷–łŖ∂Ģ—ß…ķ”–400√Ż£¨’‚»żňý—ß–£÷ģő łŖ∂Ģ—ß…ķ»ň żĶńĪ»ņżľŻ…»–őÕ≥ľ∆Õľ£ģ
£®1£©«ů»ę –łŖ∂Ģ—ß…ķ◊‹ ż£Ľ
£®2£©«ů»ę –Ĺ‚īūÕͻ꒿»∑ĶńłŖ∂Ģ—ß…ķ ż’ľłŖ∂Ģ—ß…ķ◊‹ żĶńįŔ∑÷Ī»£Ľ
£®3£©«Žń„∂‘»ż÷–łŖ∂Ģ ż—ßņŌ ¶ŐŠ“ĽłŲ÷ĶĶ√Ļō◊ĘĶńĹŐ—ßĹ®“ť£¨≤ĘňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com