练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．在⊙O中，有两条弦AB和CD，如果$\widehat{AB}$=2$\widehat{CD}$，那么弦AB和2CD的大小关系为AB＜2CD．

    分析 首先取$\widehat{AB}$的中点E，连接AE，BE，由在⊙O中，$\widehat{AB}$=2$\widehat{CD}$，可证得$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$，即可得AE=BE=CD，然后由三角形的三边关系，求得答案．

    解答 解：如图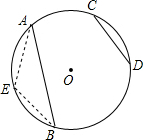，取$\widehat{AB}$的中点E，连接AE，BE，
    ∵在⊙O中，$\widehat{AB}$=2$\widehat{CD}$，
    ∴$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$，
    ∴AE=BE=CD，
    ∵AE+BE＞AB，
    ∴AB＜2CD．
    故答案为：＜．

    点评 此题考查了弧与弦的关系以及三角形的三边关系．注意在同圆或等圆中，同弧或等弧，所对的弦相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．如图所示，△ABC∽△ACD，且AD=5，BD=4，求△ACD与△ABC的相似比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列条件中，能确定圆的是（　　）
    A．以点O为圆心B．以2cm长为半径
    C．以点O为圆心，以5cm长为半径D．经过已知点A

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

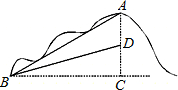    6．某山区计划修建一条通过小山的公路，经测量，如图，从山底B到山顶A的坡角是30°，斜坡AB长为100米．根据地形，要求修好的公路路面BD的坡度为i=1：5（假定A，D两点处于同一直线上）．为了减少工程量，若AD≤20米，则直接开挖修建公路；若AD＞20米，就要重新设计．问这段公路是否需要重新设计？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

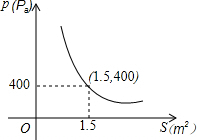    13．某校科技小组进行野外考察，途中遇到一片十几米宽的湿地．为了安全、迅速通过这片湿地，他们沿着前进路线铺若干块木板，构筑成一条临时通道，木板对地面的压强p（Pa）是木板面积S（m2）的反比例函数，其图象如图所示，当木板压强不超过6 000Pa时，木板的面积至少应为0.1m2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．已知，如图⊙O的半径OA=5cm，弦CD=5cm，则弦CD所对圆心角为60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

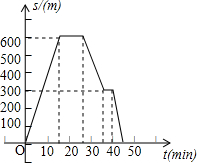    10．张爷爷晚饭以后外出散步，碰到老邻居，交谈了一会儿，返回途中在读报栏前看了一会儿报，如图是据此情境画出的图象，请你回答下面的问题：
    （1）张爷爷是在什么地方碰到老邻居的，交谈了多长时间？
    （2）读报栏大约离家多远？
    （3）图中反映了哪些变量之间的关系？其中哪个是自变量？哪个是因变量？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知2+$\sqrt{3}$是方程x2-5sinθ•x+1=0的一个根，求sinθ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．近年来，义乌市民用汽车拥有量持续增长，2007年至2011年我市民用汽车拥有量依次约为（单位：万辆）：11，13，15，19，x，这五个数的平均数为16.2，则x的值为23．

    查看答案和解析>>

    同步练习册答案