
 如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.分析 (1)连接OD,根据已知和切线的性质证明△OCD为等腰直角三角形,得到∠DOC=45°,根据S阴影=S△OCD-S扇OBD计算即可;
(2)连接AD,根据弦、弧之间的关系证明DB=DE,证明△AMD≌△ABD,得到DM=BD,得到答案.
解答 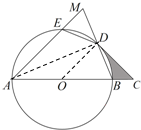 (1)解:如图,连接OD,
(1)解:如图,连接OD,
∵CD是⊙O切线,
∴OD⊥CD,
∵OA=CD=2$\sqrt{2}$,OA=OD,
∴OD=CD=2$\sqrt{2}$,
∴△OCD为等腰直角三角形,
∴∠DOC=∠C=45°,
∴S阴影=S△OCD-S扇OBD=$\frac{1}{2}×2\sqrt{2}×2\sqrt{2}$-$\frac{45π×(2\sqrt{2})^{2}}{360}$=4-π;
(2)证明:如图,连接AD,
∵AB是⊙O直径,
∴∠ADB=∠ADM=90°,
又∵$\widehat{ED}$=$\widehat{BD}$,
∴ED=BD,∠MAD=∠BAD,
在△AMD和△ABD中,
$\left\{\begin{array}{l}{∠ADM=∠ADB}\\{AD=AD}\\{∠MAD=∠BAD}\end{array}\right.$,
∴△AMD≌△ABD,
∴DM=BD,
∴DE=DM.
点评 本题考查的是切线的性质、弦、弧之间的关系、扇形面积的计算,掌握切线的性质定理和扇形的面积公式是解题的关键,注意辅助线的作法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
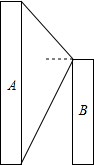 近两年房地产以开发电梯房为主,如图为某小区的电梯房,其中A楼为标志楼房,张华为测量A楼的高,站在距离A楼30米的B楼顶端,测得看A楼顶端的仰角为60°,看A楼底端的俯角为75°,请你帮张华求出A楼的高.(参考数据:sin75°=0.97,cos75°=0.26,tan75°=3.73,sin60°=0.87,cos60°=0.5,tan60°=1.73,结果精确到0.1米)
近两年房地产以开发电梯房为主,如图为某小区的电梯房,其中A楼为标志楼房,张华为测量A楼的高,站在距离A楼30米的B楼顶端,测得看A楼顶端的仰角为60°,看A楼底端的俯角为75°,请你帮张华求出A楼的高.(参考数据:sin75°=0.97,cos75°=0.26,tan75°=3.73,sin60°=0.87,cos60°=0.5,tan60°=1.73,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
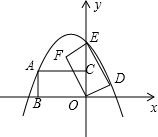 如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1,OB=$\sqrt{3}$,矩形ABOC绕点O按逆时针方向旋转60°后得到矩形EFOD,点A的对应点为点E,点B的对应点为点F.点C的对应点为点D.
如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1,OB=$\sqrt{3}$,矩形ABOC绕点O按逆时针方向旋转60°后得到矩形EFOD,点A的对应点为点E,点B的对应点为点F.点C的对应点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
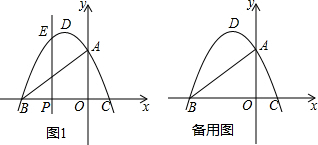
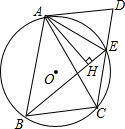 如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.
如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
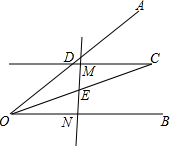 如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.
如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间(第x天) | 1 | 3 | 6 | 10 | … |
| 日销售量(m件) | 198 | 194 | 188 | 180 | … |
| 时间(第x天) | 1≤x<50 | 50≤x≤90 |
| 销售价格(元/件) | x+60 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com