
| 时间(第x天) | 1 | 3 | 6 | 10 | … |
| 日销售量(m件) | 198 | 194 | 188 | 180 | … |
| 时间(第x天) | 1≤x<50 | 50≤x≤90 |
| 销售价格(元/件) | x+60 | 100 |
分析 (1)根据待定系数法解出一次函数解析式即可;
(2)设利润为y元,则当1≤x<50时,y=-2x2+160x+4000;当50≤x≤90时,y=-120x+12000,分别求出各段上的最大值,比较即可得到结论;
(3)直接写出在该产品销售的过程中,共有46天销售利润不低于5400元.
解答 解:(1)∵m与x成一次函数,
∴设m=kx+b,将x=1,m=198,x=3,m=194代入,得:
$\left\{\begin{array}{l}{k+b=198}\\{3k+b=194}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=200}\end{array}\right.$.
所以m关于x的一次函数表达式为m=-2x+200;
(2)设销售该产品每天利润为y元,y关于x的函数表达式为:$\left\{\begin{array}{l}{y=-2{x}^{2}+160x+4000(1≤x<50)}\\{y=-120x+12000(50≤x≤90)}\end{array}\right.$,
当1≤x<50时,y=-2x2+160x+4000=-2(x-40)2+7200,
∵-2<0,
∴当x=40时,y有最大值,最大值是7200;
当50≤x≤90时,y=-120x+12000,
∵-120<0,
∴y随x增大而减小,即当x=50时,y的值最大,最大值是6000;
综上所述,当x=40时,y的值最大,最大值是7200,即在90天内该产品第40天的销售利润最大,最大利润是7200元;
(3)在该产品销售的过程中,共有46天销售利润不低于5400元.
点评 本题考查分段函数,考查函数的最值,解题的关键是正确写出分段函数的解析式,属于中档题.


科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
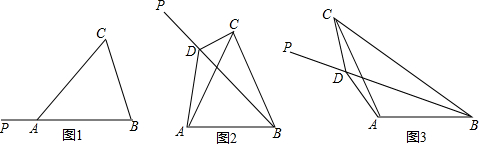
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 捐款的数额(单位:元) | 20 | 50 | 80 | 100 |
| 人数(单位:名) | 6 | 7 | 4 | 3 |
| A. | 20元 | B. | 50元 | C. | 80元 | D. | 100元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
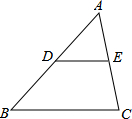 补充完整三角形中位线定理,并加以证明:
补充完整三角形中位线定理,并加以证明:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=-1 | B. | m=0 | C. | m=3 | D. | m=0或m=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
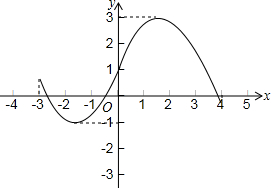 若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
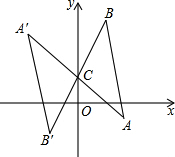 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )
如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )| A. | (-a,-b) | B. | (-a,-b+2) | C. | (-a,-b+1) | D. | (-a,-b-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com