
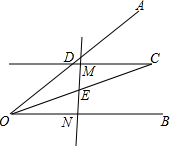
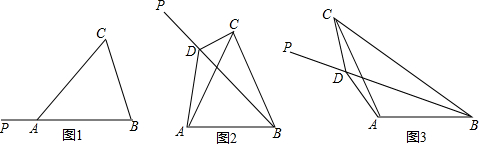
 如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.
如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论. 分析 (1)当点M在线段CD上时,线段OD、ON、DM之间的数量关系是:OD=DM+ON.首先根据OC是∠AOB的平分线,CD∥OB,判断出∠DOC=∠DC0,所以OD=CD=DM+CM;然后根据E是线段OC的中点,CD∥OB,推得CM=ON,即可判断出OD=DM+ON,据此解答即可.
(2)当点M在线段CD延长线上时,线段OD、ON、DM之间的数量关系是:OD=ON-DM.由(1),可得OD=DC=CM-DM,再根据CM=ON,推得OD=ON-DM即可.
解答 解:(1)当点M在线段CD上时,线段OD、ON、DM之间的数量关系是:OD=DM+ON.
证明:如图1,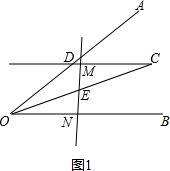 ,
,
∵OC是∠AOB的平分线,
∴∠DOC=∠C0B,
又∵CD∥OB,
∴∠DCO=∠C0B,
∴∠DOC=∠DC0,
∴OD=CD=DM+CM,
∵E是线段OC的中点,
∴CE=OE,
∵CD∥OB,
∴$\frac{CM}{ON}=\frac{CE}{OE}=1$,
∴CM=ON,
又∵OD=DM+CM,
∴OD=DM+ON.
(2)当点M在线段CD延长线上时,线段OD、ON、DM之间的数量关系是:OD=ON-DM.
证明:如图2,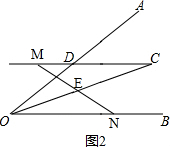 ,
,
由(1),可得
OD=DC=CM-DM,
又∵CM=ON,
∴OD=DC=CM-DM=ON-DM,
即OD=ON-DM.
点评 (1)此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.②定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.
(2)此题还考查了等腰三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等.②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2015}$ | B. | -$\frac{1}{2015}$ | C. | 2015 | D. | -2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
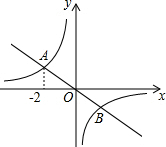 如图,双曲线y=$\frac{k}{x}$与直线y=-$\frac{1}{2}$x交于A、B两点,且A(-2,m),则点B的坐标是( )
如图,双曲线y=$\frac{k}{x}$与直线y=-$\frac{1}{2}$x交于A、B两点,且A(-2,m),则点B的坐标是( )| A. | (2,-1) | B. | (1,-2) | C. | ($\frac{1}{2}$,-1) | D. | (-1,$\frac{1}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
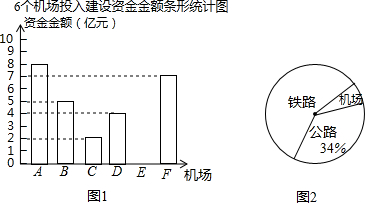
| 铁路 | 公路 | 机场 | 铁路、公路、机场三项投入建设资金总金额(亿元) | |
| 投入资金(亿元) | 300 | a | b | m |
| 所占百分比 | c | 34% | 6% | |
| 所占圆心角 | 216° | d | 21.6° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 捐款的数额(单位:元) | 20 | 50 | 80 | 100 |
| 人数(单位:名) | 6 | 7 | 4 | 3 |
| A. | 20元 | B. | 50元 | C. | 80元 | D. | 100元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
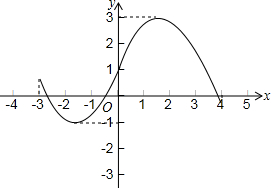 若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com