
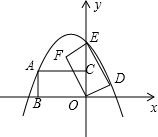
 ШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮABOCЕФБпBOдкxжсЕФИКАыжсЩЯЃЌБпOCдкyжсЕФе§АыжсЩЯЃЌЧвAB=1ЃЌOB=$\sqrt{3}$ЃЌОиаЮABOCШЦЕуOАДФцЪБеыЗНЯђа§зЊ60ЁуКѓЕУЕНОиаЮEFODЃЌЕуAЕФЖдгІЕуЮЊЕуEЃЌЕуBЕФЖдгІЕуЮЊЕуFЃЎЕуCЕФЖдгІЕуЮЊЕуDЃЎ
ШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮABOCЕФБпBOдкxжсЕФИКАыжсЩЯЃЌБпOCдкyжсЕФе§АыжсЩЯЃЌЧвAB=1ЃЌOB=$\sqrt{3}$ЃЌОиаЮABOCШЦЕуOАДФцЪБеыЗНЯђа§зЊ60ЁуКѓЕУЕНОиаЮEFODЃЌЕуAЕФЖдгІЕуЮЊЕуEЃЌЕуBЕФЖдгІЕуЮЊЕуFЃЎЕуCЕФЖдгІЕуЮЊЕуDЃЎЗжЮі ЃЈ1ЃЉПЩСЌНгOAЃЌЭЈЙ§жЄЁЯAOE=60ЁуЃЌМДгыа§зЊНЧЯрЭЌРДЕУГіOEдкyжсЩЯЕФНсТлЃЎ
ЃЈ2ЃЉвбжЊABЃЌOBЕФГЄМДПЩЧѓГіAЕФзјБъЃЌдкжБНЧШ§НЧаЮOEFжаЃЌПЩгУЙДЙЩЖЈРэЧѓГіOEЕФГЄЃЌвВОЭФмЧѓЕУEЕуЕФзјБъЃЌвЊЯыЕУГіХзЮяЯпЕФНтЮіЪНЛЙЩйDЕуЕФзјБъЃЌПЩЙ§DзїxжсЕФДЙЯпЃЌЭЈЙ§ЙЙНЈжБНЧШ§НЧаЮЃЌИљОнODЕФГЄКЭЁЯDOxЕФе§ЯвКЭгрЯвжЕРДЧѓГіDЕФзјБъЃЛЧѓГіAЁЂEЁЂDШ§ЕузјБъКѓМДПЩгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ3ЃЉПЩЯШЧѓГіОиаЮЕФУцЛ§ЃЌНјЖјПЩЕУГіЦНааЫФБпаЮOBPQЕФУцЛ§ЃЎгЩгкЦНааЫФБпаЮжаOBБпЕФГЄЪЧЖЈжЕЃЌвђДЫПЩИљОнЦНааЫФБпаЮЕФУцЛ§ЧѓГіPЕуЕФзнзјБъЃЈгЩгкPЕудкxжсЩЯЗНЃЌвђДЫPЕФзнзјБъЮЊе§Ъ§ЃЉЃЌШЛКѓНЋPЕуЕФзнзјБъДњШыХзЮяЯпжаПЩЧѓГіPЕуЕФзјБъЃЎЧѓГіPЕуЕФзјБъКѓЃЌНЋPЕуЗжБ№ЯђзѓЁЂЯђгвЦНвЦOBИіЕЅЮЛМДПЩЕУГіQЕуЕФзјБъЃЌгЩДЫПЩЕУГіЗћКЯЬѕМўЕФСНИіPЕузјБъКЭЫФИіQЕузјБъЃЎ
НтД№ 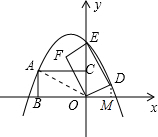 НтЃКЃЈ1ЃЉСЌНгAOЃЌШчЭМЃЌдкRTЁїABOжаЃЌ
НтЃКЃЈ1ЃЉСЌНгAOЃЌШчЭМЃЌдкRTЁїABOжаЃЌ
ЁпAB=1ЃЌBO=$\sqrt{3}$ЃЌ
ЁрAO=2ЃЌ
ЁрsinЁЯAOB=$\frac{1}{2}$ЃЌ
ЁрЁЯAOB=30ЁуЃЌ
гЩЬтвтПЩжЊЃКЁЯAOE=60ЁуЃЌ
ЁрЁЯBOE=ЁЯAOB+ЁЯADE=30Ёу+60Ёу=90ЁуЃЌ
ЁпБпBOдкxжсЕФИКАыжсЩЯЃЌ
ЁрEдкyжсЕФе§АыжсЩЯЃЌ
гжЁпEO=AO=2ЃЌ
ЁрЕуEЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЃЛ
ЃЈ2ЃЉЙ§ЕуDзїDMЁЭxжсгкЕуMЃЌ
ЁпOD=1ЃЌЁЯDOM=30ЁуЃЌ
ЁрдкRTЁїDOMжаЃЌDM=$\frac{1}{2}$ЃЌOM=$\frac{\sqrt{3}}{2}$ЃЌ
ЁпЕуDдкЕквЛЯѓЯоЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ$\frac{\sqrt{3}}{2}$ЃЌ$\frac{1}{2}$ЃЉЃЌ
ЁпAO=2ЃЌЕуAдкЕкЖўЯѓЯоЃЌ
ЁрЕуAЕФзјБъЮЊЃЈ-$\sqrt{3}$ЃЌ1ЃЉ
ЁпЩшЙ§ЕуAЃЌEЃЌDЕФХзЮяЯпЮЊy=ax2+bx+cЃЌ
ЁпОЙ§ЕуEЃЌ
Ёрc=2
гЩЬтвтЃЌНЋAЃЈ-$\sqrt{3}$ЃЌ1ЃЉЃЌDЃЈ$\frac{\sqrt{3}}{2}$ЃЌ$\frac{1}{2}$ЃЉДњШыy=ax2+bx+2жаЃЌЕУ$\left\{\begin{array}{l}{3a-\sqrt{3}b+2=1}\\{\frac{3}{4}a+\frac{\sqrt{3}}{2}b+2=\frac{1}{2}}\end{array}\right.$ЃЌ
НтЕУ$\left\{\begin{array}{l}{a=-\frac{8}{9}}\\{b=-\frac{5\sqrt{3}}{9}}\end{array}\right.$ЃЎ
ЁрЫљЧѓХзЮяЯпБэДяЪНЮЊЃКy=-$\frac{8}{9}$x2-$\frac{5\sqrt{3}}{9}$x+2ЃЛ
ЃЈ3ЃЉДцдкЗћКЯЬѕМўЕФЕуPЃЌЕуQЃЎ
РэгЩШчЯТЃКЁпОиаЮABOCЕФУцЛ§=AB•BO=$\sqrt{3}$ЃЌ
ЁрвдOЃЌBЃЌPЃЌQЮЊЖЅЕуЕФЦНааЫФБпаЮУцЛ§ЮЊ2$\sqrt{3}$ЃЎ
гЩЬтвтПЩжЊOBЮЊДЫЦНааЫФБпаЮвЛБпЃЌ
гжЁпOB=$\sqrt{3}$ЃЌ
ЁрOBБпЩЯЕФИпЮЊ2ЃЌ
вРЬтвтЩшЕуPЕФзјБъЮЊЃЈmЃЌ2ЃЉЃЌ
ЁпЕуPдкХзЮяЯпy=-$\frac{8}{9}$x2-$\frac{5\sqrt{3}}{9}$x+2ЩЯЃЌ
-$\frac{8}{9}$m2-$\frac{5\sqrt{3}}{9}$m+2=2ЃЌ
НтЕУЃЌm1=0ЃЌm2=-$\frac{5\sqrt{3}}{8}$ЃЌ
ЁрP1ЃЈ0ЃЌ2ЃЉЃЌP2ЃЈ-$\frac{5\sqrt{3}}{8}$ЃЌ2ЃЉЃЌ
ЁпвдOЃЌBЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌ
ЁрPQЁЮOBЃЌPQ=OB=$\sqrt{3}$ЃЌ
ЁрЕБЕуP1ЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЪБЃЌЕуQЕФзјБъЗжБ№ЮЊQ1ЃЈ-$\sqrt{3}$ЃЌ2ЃЉЃЌQ2ЃЈ$\sqrt{3}$ЃЌ2ЃЉЃЛ
ЕБЕуP2ЕФзјБъЮЊЃЈ-$\frac{5\sqrt{3}}{8}$ЃЌ2ЃЉЪБЃЌЕуQЕФзјБъЗжБ№ЮЊQ3ЃЈ-$\frac{13\sqrt{3}}{8}$ЃЌ2ЃЉЃЌQ4ЃЈ$\frac{3\sqrt{3}}{8}$ЃЌ2ЃЉЃЎ
ЕуЦР БОЬтзХжиПМВщСЫД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪНЁЂЭМаЮа§зЊБфЛЛЁЂЦНааЫФБпаЮЕФаджЪЕШжЊЪЖЕуЃЌзлКЯадЧПЃЌФмСІвЊЧѓНЯИпЃЎПМВщбЇЩњЪ§аЮНсКЯЕФЪ§бЇЫМЯыЗНЗЈЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
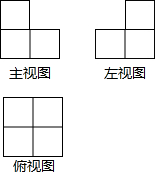 ШчЭМЪЧгЩРтГЄЮЊ1cmЕФаЁСЂЗНПщзщГЩЕФМИКЮЬхЕФШ§ЪгЭМЃЌетИіМИКЮЬхЕФБэУцЛ§ЪЧ20cm2ЃЎ
ШчЭМЪЧгЩРтГЄЮЊ1cmЕФаЁСЂЗНПщзщГЩЕФМИКЮЬхЕФШ§ЪгЭМЃЌетИіМИКЮЬхЕФБэУцЛ§ЪЧ20cm2ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
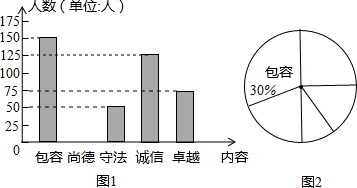
 ШчЭМЪЧвЛИіАыдВаЮЧХЖДЕФНиУцЪОвтЭМЃЌдВаФЮЊOЃЌжБОЖABЪЧКгЕзЯпЃЌЯвCDЪЧЫЎЮЛЯпЃЌCDЁЮABЃЌЧвCD=24cmЃЌOEЁЭCDгкЕуEЃЌЯжВтЕУsinЁЯDOE=$\frac{12}{13}$ЃЌдђЫЎЩюЪЧ5mЃЎ
ШчЭМЪЧвЛИіАыдВаЮЧХЖДЕФНиУцЪОвтЭМЃЌдВаФЮЊOЃЌжБОЖABЪЧКгЕзЯпЃЌЯвCDЪЧЫЎЮЛЯпЃЌCDЁЮABЃЌЧвCD=24cmЃЌOEЁЭCDгкЕуEЃЌЯжВтЕУsinЁЯDOE=$\frac{12}{13}$ЃЌдђЫЎЩюЪЧ5mЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌ$\widehat{ED}$=$\widehat{BD}$ЃЌСЌНгEDЁЂBDЃЌбгГЄAEНЛBDЕФбгГЄЯпгкЕуMЃЌЙ§ЕуDзїЁбOЕФЧаЯпНЛABЕФбгГЄЯпгкЕуCЃЎ
ШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌ$\widehat{ED}$=$\widehat{BD}$ЃЌСЌНгEDЁЂBDЃЌбгГЄAEНЛBDЕФбгГЄЯпгкЕуMЃЌЙ§ЕуDзїЁбOЕФЧаЯпНЛABЕФбгГЄЯпгкЕуCЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
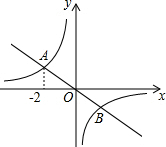 ШчЭМЃЌЫЋЧњЯпy=$\frac{k}{x}$гыжБЯпy=-$\frac{1}{2}$xНЛгкAЁЂBСНЕуЃЌЧвAЃЈ-2ЃЌmЃЉЃЌдђЕуBЕФзјБъЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌЫЋЧњЯпy=$\frac{k}{x}$гыжБЯпy=-$\frac{1}{2}$xНЛгкAЁЂBСНЕуЃЌЧвAЃЈ-2ЃЌmЃЉЃЌдђЕуBЕФзјБъЪЧЃЈЁЁЁЁЃЉ| AЃЎ | ЃЈ2ЃЌ-1ЃЉ | BЃЎ | ЃЈ1ЃЌ-2ЃЉ | CЃЎ | ЃЈ$\frac{1}{2}$ЃЌ-1ЃЉ | DЃЎ | ЃЈ-1ЃЌ$\frac{1}{2}$ЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
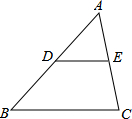 ВЙГфЭъећШ§НЧаЮжаЮЛЯпЖЈРэЃЌВЂМгвджЄУїЃК
ВЙГфЭъећШ§НЧаЮжаЮЛЯпЖЈРэЃЌВЂМгвджЄУїЃКВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com